Fonction de Transfert et Analyse

Transformée de Laplace

Pour analyser les systèmes SLIT, la transformée de Laplace offre plusieurs avantages par rapport à l'utilisation directe d'équations différentielles. En effet, cette transformée permet de transformer des équations différentielles en équations algébriques, plus simples à manipuler.

Définition

Transformée de Laplace

La transformée de Laplace est définie comme une transformation intégrale qui convertit une fonction temporelle $f(t)$ en une fonction de la variable complexe $s$. Mathématiquement, la transformée de Laplace monolatérale s'exprime sous la forme:

$$F(s)=\mathcal{L}\{f(t)\}={\int }_0^{\mathrm{\infty }}f(t)e^{-st}dt$$

où $s$ est une variable complexe $s=\sigma +j\omega$, avec $\sigma$ représentant la partie réelle et $\omega$ la partie imaginaire.

Transformée de Laplace Inverse

La transformée de Laplace inverse est une transformation qui permet de revenir du domaine de Laplace au domaine temporel.

$$f(t)={\mathcal{L}}^{-1}\{F(s)\}=\frac{1}{2\pi j}{\int }_{\sigma -j\mathrm{\infty }}^{\sigma +j\mathrm{\infty }}F(s)e^{st}ds$$

En pratique, la transformée de Laplace inverse sera le plus souvent obtenue en utilisant des tables.

Exemples

Signal échelon

Considérons la fonction échelon unitaire $x(t)=u(t)$. Pour $t\ge 0$, $x(t)=1$, la transformée de Laplace est donc égale à :

$$X(s)=\mathcal{L}\{u(t)\}={\int }_0^{\mathrm{\infty }}1\cdot e^{-st}dt={\int }_0^{\mathrm{\infty }}{e}^{-st}dt$$

Rappelons que l'intégrale de $e^{-st}$ est :

$$\int e^{-st}dt=-\frac{1}{s}{e}^{-st}$$

En évaluant cette expression entre les bornes $0$ et $\mathrm{\infty }$, nous obtenons

$${[-\frac{1}{s}{e}^{-st}]}_0^{\mathrm{\infty }}=(-\frac{1}{s}{e}^{-s\cdot \mathrm{\infty }})-(-\frac{1}{s}{e}^{-s\cdot 0})$$

• Lorsque $t\to \mathrm{\infty }$, $e^{-st}\to 0$ si $\text{Re}(s)>0$.
• Lorsque $t=0$, $e^{-st}=e^0=1$.

Pour $\text{Re}(s)>0$, l'intégrale converge et est égale à :

$$X(s)={\int }_0^{\mathrm{\infty }}1\cdot e^{-st}dt={\int }_0^{\mathrm{\infty }}{e}^{-st}dt=\frac{1}{s}$$

Signal Exponentiel

Considérons le signal exponentiel $x(t)=e^{-at}u(t)$. En utilisant la définition de la transformée de Laplace, nous obtenons :

$$X(s)=\mathcal{L}\{x(t)\}={\int }_0^{\mathrm{\infty }}{e}^{-at}{e}^{-st}dt={\int }_0^{\mathrm{\infty }}{e}^{-(s+a)t}dt$$

Nous obtenons alors

$$X(s)={\left[\frac{1}{s+a}{e}^{-(s+a)t}\right]}_0^{\mathrm{\infty }}=\frac{1}{s+a}$$

Les transformées de Laplace des signaux usuels sont souvent présentées dans une table.

Propriétés

La transformée de Laplace possède plusieurs propriétés qui permettent de simplifier significativement l'analyse des systèmes SLIT.

1. Linéarité

La transformée de Laplace est une opération linéaire :

$$\mathcal{L}\{af(t)+bg(t)\}=a\mathcal{L}\{f(t)\}+b\mathcal{L}\{g(t)\}$$

où $a$ et $b$ sont des constantes, et $f(t)$ et $g(t)$ sont des fonctions de $t$.

Démonstration

Pour démontrer cette propriété, nous devons appliquer la définition de la transformée de Laplace à la fonction $af(t)+bg(t)$.

$$\begin{array}{rl}\mathcal{L}\{af(t)+bg(t)\}& ={\int }_0^{\mathrm{\infty }}(af(t)+bg(t))e^{-st}dt\\ & ={\int }_0^{\mathrm{\infty }}af(t)e^{-st}dt+{\int }_0^{\mathrm{\infty }}bg(t)e^{-st}dt\\ & =a{\int }_0^{\mathrm{\infty }}f(t)e^{-st}dt+b{\int }_0^{\mathrm{\infty }}g(t)e^{-st}dt\\ & =a\mathcal{L}\{f(t)\}+b\mathcal{L}\{g(t)\}\end{array}$$

2. Dérivation

La transformée de Laplace de la dérivée d'une fonction est donnée par :

$$\mathcal{L}\left\{\frac{d^{n}f(t)}{d{t}^n}\right\}=s^{n}F(s)-s^{n-1}f(0^{-})-s^{n-2}{f}^{\prime }(0^{-})-\cdots -f^{(n-1)}(0^{-})$$

où $F(s)$ est la transformée de Laplace de $f(t)$ et $f^{(n)}(0^{-})$ représente la $n$-ième dérivée de $f(t)$ évaluée à $t=0^{-}$.

TIP

Lorsque toutes les conditions initiales sont nulles, $f^{(n)}(0)=0$ et donc

$$\mathcal{L}\left\{\frac{d^{n}f(t)}{d{t}^n}\right\}=s^{n}F(s)$$

Démonstration

Nous allons démontrer ici la propriété pour $n=1$. La démonstration pour les autres valeurs de $n$ s'obtient par induction.

La transformée de Laplace de $f^{\prime }(t)$ est définie par :

$$\mathcal{L}\{f^{\prime }(t)\}={\int }_0^{\mathrm{\infty }}{f}^{\prime }(t)e^{-st}dt$$

En utilisant l'intégration par parties, avec $u=e^{-st}$ et $dv=f^{\prime }(t)dt$, nous avons :

$$du=-s{e}^{-st}dt\text{et}v=f(t)$$

Ainsi, l'intégration par parties donne :

$${\int }_0^{\mathrm{\infty }}{f}^{\prime }(t)e^{-st}dt={[f(t)e^{-st}]}_0^{\mathrm{\infty }}+s{\int }_0^{\mathrm{\infty }}f(t)e^{-st}dt$$

Évaluons le premier terme ${[f(t)e^{-st}]}_0^{\mathrm{\infty }}$:

• À $t\to \mathrm{\infty }$, si $f(t)$ ne croît pas plus vite qu'une exponentielle, $f(t)e^{-st}\to 0$.
• À $t=0$, $f(0)e^{-s\cdot 0}=f(0)$.

Donc :

$${[f(t)e^{-st}]}_0^{\mathrm{\infty }}=0-f(0)=-f(0)$$

Ainsi, nous avons :

$$\mathcal{L}\{f^{\prime }(t)\}=-f(0)+s{\int }_0^{\mathrm{\infty }}f(t)e^{-st}dt=-f(0)+s\mathcal{L}\{f(t)\}$$

Donc :

$$\mathcal{L}\{f^{\prime }(t)\}=sF(s)-f(0)$$

3. Intégration

La transformée de Laplace de l'intégrale d'une fonction est donnée par :

$$\mathcal{L}\{{\int }_0^{t}f(\tau )d\tau \}=\frac{F(s)}{s}$$

4. Théorème du décalage dans le temps

Si une fonction $f(t)$ est décalée dans le temps de $t_0$ unités, la transformée de Laplace est modifiée comme suit :

$$\mathcal{L}\{f(t-t_0)u(t-t_0)\}=e^{-s{t}_0}F(s)$$

où $u(t)$ est la fonction échelon.

Démonstration

Nous voulons trouver la transformée de Laplace de $f(t-t_0)u(t-t_0)$ où $u(t)$ est la fonction échelon unitaire. La fonction $f(t-t_0)u(t-t_0)$ est donc nulle pour $t<t_0$ et égale à $f(t-t_0)$ pour $t\ge t_0$. Nous calculons la transformée de Laplace de $f(t-t_0)u(t-t_0)$ en utilisant la définition :

$$\mathcal{L}\{f(t-t_0)u(t-t_0)\}={\int }_0^{\mathrm{\infty }}f(t-t_0)u(t-t_0)e^{-st}dt$$

Comme $f(t-t_0)u(t-t_0)$ est nul pour $t<t_0$, nous pouvons changer les bornes d'intégration de $0$ à $t_0$ en $t_0$ à $\mathrm{\infty }$:

$$\mathcal{L}\{f(t-t_0)u(t-t_0)\}={\int }_{t_0}^{\mathrm{\infty }}f(t-t_0)e^{-st}dt$$

Pour simplifier cette intégrale, nous faisons un changement de variable. Posons $\tau =t-t_0$. Alors $dt=d\tau$ et lorsque $t$ varie de $t_0$ à $\mathrm{\infty }$, $\tau$ varie de $0$ à $\mathrm{\infty }$. L'intégrale devient :

$$\mathcal{L}\{f(t-t_0)u(t-t_0)\}={\int }_0^{\mathrm{\infty }}f(\tau )e^{-s(\tau +t_0)}d\tau$$

Nous pouvons séparer le facteur exponentiel en deux termes :

$$\mathcal{L}\{f(t-t_0)u(t-t_0)\}={\int }_0^{\mathrm{\infty }}f(\tau )e^{-s\tau }{e}^{-s{t}_0}d\tau$$

Comme $e^{-s{t}_0}$ est indépendant de $\tau$, nous pouvons le sortir de l'intégrale :

$$\mathcal{L}\{f(t-t_0)u(t-t_0)\}=e^{-s{t}_0}{\int }_0^{\mathrm{\infty }}f(\tau )e^{-s\tau }d\tau$$

L'intégrale ${\int }_0^{\mathrm{\infty }}f(\tau )e^{-s\tau }d\tau$ est la définition de la transformée de Laplace de $f(t)$, que nous avons notée $F(s)$. Donc :

$$\mathcal{L}\{f(t-t_0)u(t-t_0)\}=e^{-s{t}_0}F(s)$$

5. Multiplication par une exponentielle

La multiplication d'une fonction par une exponentielle se traduit par un décalage dans le domaine de la transformée de Laplace :

$$\mathcal{L}\{e^{at}f(t)\}=F(s-a)$$

6. Théorème de convolution

La transformée de Laplace de la convolution de deux fonctions est le produit des transformées de Laplace de ces fonctions :

$$\mathcal{L}\{(f\ast g)(t)\}=F(s)G(s)$$

où $(f\ast g)(t)={\int }_0^{t}f(\tau )g(t-\tau )d\tau$.

7. Valeur initiale et valeur finale

• Théorème de la valeur initiale :

$$f(0^{+})=\underset{t\to 0^{+}}{lim}f(t)=\underset{s\to \mathrm{\infty }}{lim}sF(s)$$

• Théorème de la valeur finale :

$$f(\mathrm{\infty })=\underset{t\to \mathrm{\infty }}{lim}f(t)=\underset{s\to 0}{lim}sF(s)$$

Démonstration

Les deux démonstrations reposent sur la propriété de dérivation. Soit $g(t)=\frac{df(t)}{dt}$. En utilisant la définition de la transformée de Laplace, nous obtenons :

$$G(s)={\int }_0^{\mathrm{\infty }}g(t)e^{-st}dt$$

Par ailleurs, la propriété de dérivation en transformée de Laplace s'écrit :

$$G(s)=\mathcal{L}(g(t))=sF(s)-f(0^{-})$$

• Valeur finale. Lorsque $s\to 0$, nous obtenons dans la première égalité :

$$\underset{s\to 0}{lim}G(s)=\underset{s\to 0}{lim}{\int }_{0^{-}}^{\mathrm{\infty }}g(t)e^{-st}dt={[f(t)]}_{0^{-}}^{\mathrm{\infty }}=f(\mathrm{\infty })-f(0^{-})$$

De plus, en utilisant la seconde égalité, nous obtenons :

$$\underset{s\to 0}{lim}G(s)=\underset{s\to 0}{lim}sF(s)-f(0^{-})$$

En regroupant les deux égalités, il en vient que $f(\mathrm{\infty })=\underset{s\to 0}{lim}sF(s)$.

• Valeur initiale. Lorsque $s\to \mathrm{\infty }$, nous obtenons dans la première égalité :

$$\underset{s\to \mathrm{\infty }}{lim}G(s)=\underset{s\to \mathrm{\infty }}{lim}{\int }_{0^{-}}^{\mathrm{\infty }}\frac{df(t)}{dt}{e}^{-st}dt$$

En utilisant une intégration par partie, il est possible d'établir que :

$$\underset{s\to \mathrm{\infty }}{lim}G(s)=f(0^{+})-f(0^{-})$$

De plus, en utilisant la seconde égalité, nous obtenons :

$$\underset{s\to \mathrm{\infty }}{lim}G(s)=\underset{s\to \mathrm{\infty }}{lim}sF(s)-f(0^{-})$$

En regroupant les deux égalités, il en vient que $f(0^{+})=\underset{s\to \mathrm{\infty }}{lim}sF(s)$.

Impédances généralisées

Un avantage majeur de la transformée de Laplace est qu'elle permet d'introduire la notion d'impédance généralisée pour les composants électroniques. Cette notion simplifie considérablement l'analyse des circuits électroniques.

Composants passifs

Pour un composant passif, la relation entre la tension $v(t)$ à ses bornes et le courant $i(t)$ qui le traverse peut s'exprimer dans le domaine de Laplace par :

$$V(s)=Z(s)I(s)$$

où $Z(s)$ est l'impédance généralisée du composant.

Résistance

Pour une résistance $R$ :

$$v(t)=Ri(t)\Rightarrow Z_R(s)=R$$

Condensateur

Pour un condensateur $C$ (avec condition initiale nulle) :

$$i(t)=C\frac{dv(t)}{dt}\Rightarrow Z_C(s)=\frac{1}{Cs}$$

Bobine

Pour une bobine $L$ (avec condition initiale nulle) :

$$v(t)=L\frac{di(t)}{dt}\Rightarrow Z_L(s)=Ls$$

Lois de Kirchhoff dans le domaine de Laplace

Les lois de Kirchhoff s'appliquent directement dans le domaine de Laplace :

• Loi des nœuds : La somme des courants entrant dans un nœud est égale à la somme des courants sortants.
• Loi des mailles : La somme des tensions le long d'une maille fermée est nulle.

Exemple : Circuit RC

Considérons un circuit RC série avec :

• Une résistance $R$
• Un condensateur $C$
• Tension d'entrée $v_e(t)$
• Tension de sortie $v_s(t)$ aux bornes du condensateur

En utilisant la loi des mailles dans le domaine de Laplace :

$$V_e(s)=RI(s)+V_s(s)$$

Avec $I(s)=Cs{V}_s(s)$, nous obtenons :

$$V_e(s)=RCs{V}_s(s)+V_s(s)=(RCs+1)V_s(s)$$

La fonction de transfert est donc :

$$H(s)=\frac{V_s(s)}{V_e(s)}=\frac{1}{RCs+1}$$

Cette approche par impédances généralisées permet d'obtenir directement la fonction de transfert sans avoir à résoudre l'équation différentielle.

Fonction de transfert

Définition

La fonction de transfert du système est définie par :

$$H(s)=\frac{Y(s)}{X(s)}$$

• $s\in \mathbb{C}$ désigne la variable de Laplace,
• $X(s)=\mathcal{L}[x(t)]$ désigne la transformée de Laplace de l'entrée,
• $Y(s)=\mathcal{L}[y(t)]$ désigne la transformée de Laplace de la sortie.

L'expression de $H(s)$ peut s'obtenir

• à partir de l'équation différentielle en appliquant la transformée de Laplace sous l'hypothèse où les conditions initiales sont nulles,
• à partir de l'analyse d'un circuit électronique en utilisant directement la notion d'impédance généralisée.

Exemple 1 - À partir d'une équation différentielle

Soit l'équation différentielle de second ordre suivante :

$$a_2\frac{d^{2}y(t)}{d{t}^2}+a_1\frac{dy(t)}{dt}+a_{0}y(t)=b_{0}x(t)$$

En supposant les conditions initiales nulles, nous obtenons dans le domaine de Laplace l'équation algébrique suivante :

$$a_2{s}^{2}Y(s)+a_{1}sY(s)+a_{0}Y(s)=b_{0}X(s)$$

En factorisant de deux côtés, il en vient que :

$$(a_2{s}^2+a_{1}s+a_0)Y(s)=b_{0}X(s)\Rightarrow H(s)=\frac{b_0}{a_2{s}^2+a_{1}s+a_0}$$

Exemple 2 - À partir d'un circuit électronique

Considérons un filtre RC passe-bas avec résistance $R$ et condensateur $C$ en série. En utilisant les impédances généralisées :

• $Z_R(s)=R$
• $Z_C(s)=\frac{1}{Cs}$

Par un diviseur de tension :

$$H(s)=\frac{V_s(s)}{V_e(s)}=\frac{Z_C(s)}{Z_R(s)+Z_C(s)}=\frac{\frac{1}{Cs}}{R+\frac{1}{Cs}}=\frac{1}{RCs+1}$$

Formes générales

Soit une équation différentielle linéaire à coefficients constants d'ordre $n$. En utilisant les propriétés de linéarité et de dérivation de la transformée de Laplace et en supposant les conditions initiales nulles, nous obtenons :

$$a_n{s}^{n}Y(s)+\cdots +a_{1}sY(s)+a_{0}Y(s)=b_m{s}^{m}X(s)+\cdots +b_{1}sX(s)+b_{0}X(s)$$

En factorisant, nous obtenons :

$$Y(s)(a_n{s}^n+\cdots +a_{1}s+a_0)=X(s)(b_m{s}^m+\cdots +b_{1}s+b_0)$$

La fonction de transfert est alors égale à

$$H(s)=\frac{Y(s)}{X(s)}=\frac{b_m{s}^m+\cdots +b_{1}s+b_0}{a_n{s}^n+\cdots +a_{1}s+a_0}$$

Forme Polynomiale [ba]

$$H(s)=\frac{N(s)}{D(s)}=\frac{b_m{s}^m+\cdots +b_{1}s+b_0}{a_n{s}^n+\cdots +a_{1}s+a_0}$$

En général, pour un système causal, le degré du numérateur $m$ ne peut pas être strictement plus élevé que celui du dénominateur $n$. Nous vérifierons donc systématiquement que $m\le n$.

Fonction de transfert propre / impropre

Si $m=n$, la fonction de transfert est une fonction rationnelle impropre (c'est-à-dire le degré du numérateur est supérieur ou égal à celui du dénominateur). Dans ce contexte, il peut être utile de décomposer $H(s)$ sous la forme :

$$H(s)=H_{\mathrm{\infty }}+H_1(s)$$

où $H_{\mathrm{\infty }}$ est une constante et $H_1(s)$ est la partie strictement propre de la fonction de transfert, c'est-à-dire une fraction rationnelle dont le degré du numérateur est strictement inférieur à celui du dénominateur.

Forme Factorisée [zpk]

Le passage à la forme factorisée s'obtient en évaluant les racines du polynôme au numérateur et au dénominateur.

$$H(s)=G\frac{(s-z_m)\times \cdots \times (s-z_1)}{(s-p_n)\times \cdots \times (s-p_1)}$$

• le paramètre $G=\frac{b_m}{a_n}$ est un coefficient d'amplification,
• les zéros $z_l$ correspondent aux racines du numérateur c-à-d aux solutions de l'équation

$$b_m{s}^m+\cdots +b_{1}s+b_0=0$$

• les pôles $p_l$ correspondent aux racines du dénominateur c-à-d aux solutions de l'équation

$$a_n{s}^n+\cdots +a_{1}s+a_0=0$$

INFO

Les pôles correspondent également aux racines du polynôme caractéristique de l'équation différentielle.

Forme SOS [sos]

Lorsque les pôles ont un ordre de multiplicité maximum de 2, il est possible de décomposer la fonction de transfert comme une multiplication de fonctions de transfert de 1er et 2nd ordres:

$$H(s)=G\left(\prod _{n=1}^{n_r}\frac{N_n(s)}{s-p_n}\right)\left(\prod _{l=1}^{n_c/2}\frac{N_l(s)}{s^2-2\text{Re}(p_l)+|p_l{|}^2}\right)$$

• $p_n$ désigne un pôle réel,
• $p_l$ désigne un pôle complexe-conjugué,
• $n=n_r+n_c$ désigne l'ordre du système.

Diagramme des pôles et zéros

Le diagramme des pôles et zéros présente graphiquement la localisation des pôles ($\times$) et des zéros ($\circ$) dans le plan complexe.

Localisation des pôles et des zéros

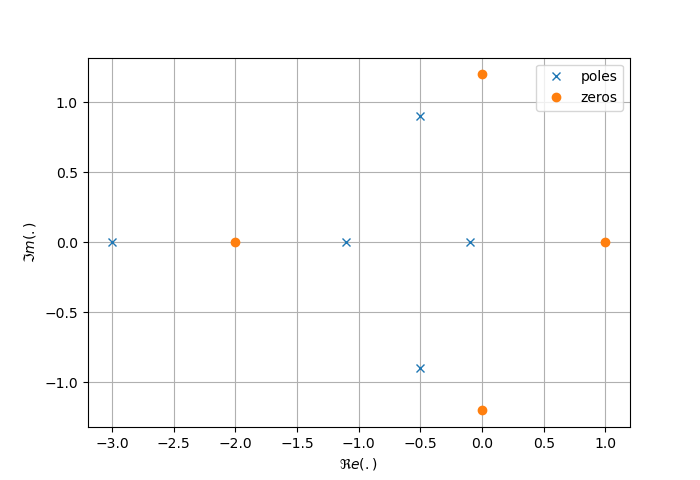
Le diagramme des pôles et zéros est très utilisé pour les raisons suivantes :

• Interprétation physique: Chaque zéro et pôle de la fonction de transfert a une signification physique associée au comportement dynamique du système. Par exemple, un pôle indique une fréquence naturelle du système et peut être lié à des phénomènes tels que la résonance. Cette représentation donne ainsi une vision intuitive du comportement du système.
• Simplification mathématique: Dans certains cas, il est plus simple et plus direct de travailler avec des zéros et des pôles plutôt qu'avec des polynômes complets, notamment lorsqu'on veut analyser la stabilité d'un système.
• Multiplication et division: Dans le cadre de la mise en série ou en parallèle de systèmes, il est souvent plus simple de multiplier ou diviser directement les représentations zpk entre elles plutôt que leurs formes polynomiales.

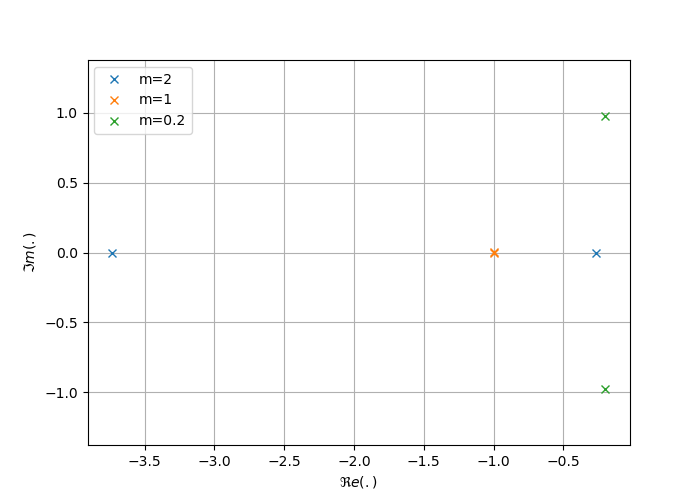
Exemple

Déterminons les pôles et zéros de la fonction de transfert de 2ème ordre suivante :

$$H(s)=\frac{K}{\frac{1}{{\omega }_0^2}{s}^2+\frac{2m}{{\omega }_0}s+1}$$

Cette fonction de transfert ne possède pas de zéro. Les pôles $p_1$ et $p_2$ s'obtiennent en cherchant les solutions de l'équation

$$\frac{1}{{\omega }_0^2}{p}^2+\frac{2m}{{\omega }_0}p+1=0$$

Le discriminant est égal à

$$\mathrm{\Delta }=\frac{4m^2}{{\omega }_0^2}-\frac{4}{{\omega }_0^2}=\frac{4}{{\omega }_0^2}(m^2-1)$$

Suivant la valeur de $\mathrm{\Delta }$, nous obtenons 3 cas de figure :

• Cas où $m>1$ : Dans ce cas, le discriminant est positif et nous obtenons deux pôles réels négatifs :

$$\begin{array}{rl}{p}_1& =-(m-\sqrt{m^2-1}){\omega }_0\\ p_2& =-(m+\sqrt{m^2-1}){\omega }_0\end{array}$$

• Cas où $m=1$: Dans ce cas, le discriminant est nul et nous obtenons un pôle double (multiplicité d'ordre 2) en

$$p_1=p_2=-{\omega }_{0}m$$

• Cas où $m<1$: Dans ce cas, le discriminant est négatif et nous obtenons deux pôles complexes-conjugués en :

$$\begin{array}{rl}{p}_1& =-(m-j\sqrt{1-m^2}){\omega }_0\\ p_2& =-(m+j\sqrt{1-m^2}){\omega }_0\end{array}$$

La figure suivante présente le diagramme des pôles pour les 3 cas.

Pôles de 3 systèmes de second ordre

Analyse temporelle

Méthodologie

Pour déterminer la sortie du système à une entrée quelconque, il est possible d'utiliser la méthodologie suivante :

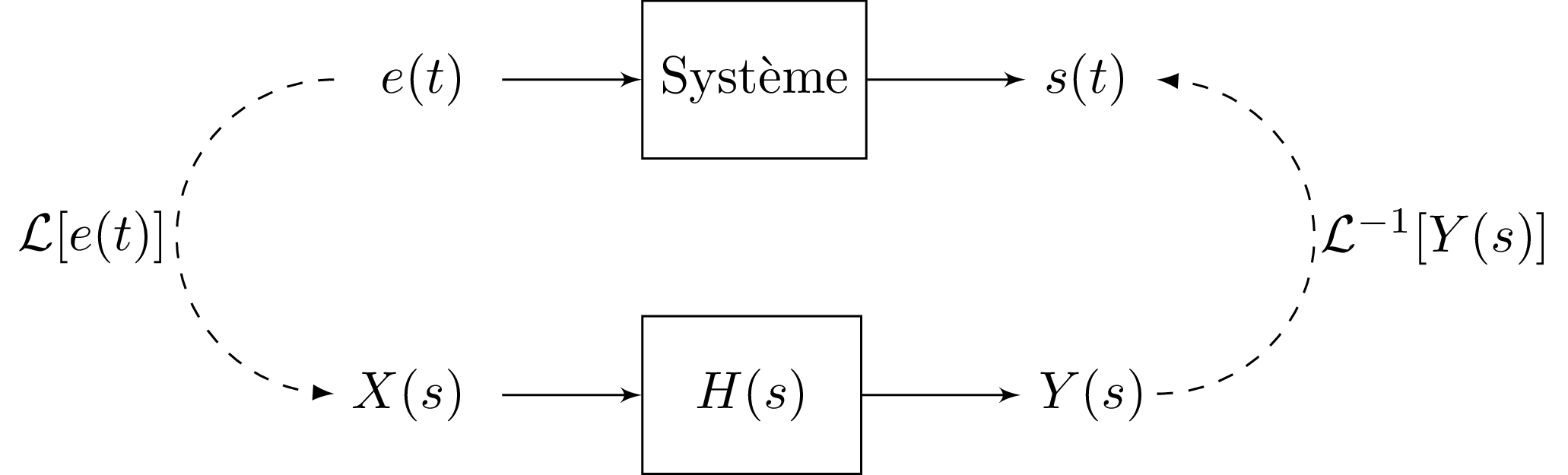
1. Détermination de $X(s)=\mathcal{L}[x(t)]$,
2. Détermination de la fonction de transfert $H(s)=\frac{Y(s)}{X(s)}$,
3. Calcul de $Y(s)=H(s)X(s)$,
4. Décomposition en éléments simples de $Y(s)$,
5. Détermination de la sortie $y(t)={\mathcal{L}}^{-1}[Y(s)]$.

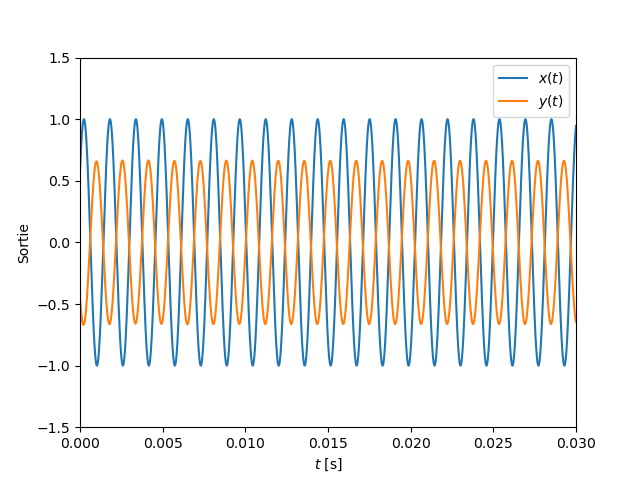
Exemple

Déterminons la réponse indicielle ($x(t)=u(t)$) de la fonction de transfert de premier ordre suivante :

$$H(s)=\frac{2}{4s+1}$$

1. La transformée de Laplace de l'entrée est égale à $X(s)=\frac{1}{s}$ (voir table)
2. La fonction de transfert est déjà déterminée,
3. La transformée de Laplace de la sortie est égale à

$$Y(s)=\frac{2}{s(4s+1)}$$

4. En utilisant une décomposition en éléments simples, cette transformée peut se décomposer sous la forme :

$$Y(s)=\frac{c_1}{s}+\frac{c_2}{4s+1}$$

• $c_1={sY(s)|}_{s=0}=2$
• $c_2={(4s+1)Y(s)|}_{s=-\frac{1}{4}}=-2\times 4=-8$

5. La sortie s'exprime alors sous la forme :

$$y(t)={\mathcal{L}}^{-1}[Y(s)]=2{\mathcal{L}}^{-1}\left[\frac{1}{s}\right]-2{\mathcal{L}}^{-1}\left[\frac{1}{s+\frac{1}{4}}\right]$$

En utilisant les tables des transformées, nous obtenons pour $t\ge 0$:

$$y(t)=2(1-e^{-\frac{1}{4}t})$$

Stabilité

Pour qu'un système soit asymptotiquement stable, il faut et il suffit que la réponse libre $y_l(t)$ converge asymptotiquement vers 0. Pour un système d'ordre $n$, le régime libre s'exprime sous la forme $y_l=\sum _{k=1}^n{\lambda }_k{e}^{p_{k}t}$. Ainsi, le système est stable si tous les pôles sont à partie réelle négative c-à-d :

$$\text{Re}(p_k)<0,\text{ pour }k=1,\dots ,n.$$

Valeur Initiale

Le théorème de la valeur initiale permet d'obtenir rapidement la sortie initiale d'un système. Mathématiquement, la sortie initiale s'exprime sous la forme :

$$y(0^{+})=\underset{t\to 0^{+}}{lim}y(t)=\underset{s\to \mathrm{\infty }}{lim}sH(s)X(s)$$

Valeur Finale

Lorsque la sortie converge vers une valeur finie, le théorème de la valeur finale permet d'obtenir rapidement cette valeur :

$$y(\mathrm{\infty })=\underset{t\to \mathrm{\infty }}{lim}y(t)=\underset{s\to 0}{lim}sH(s)X(s)$$

INFO

Lorsque l'entrée est un échelon $x(t)=Eu(t)$, il est possible d'établir que $y(\mathrm{\infty })=H(0)E$ où $H(0)$ correspond au gain statique du système.

Analyse Fréquentielle

Les exponentielles complexes de la forme $x(t)=e^{j\omega t}$ possèdent la particularité d'être des fonctions propres des systèmes SLIT. Cela signifie que si l'entrée d'un tel système est une exponentielle complexe, la sortie du système en régime permanent sera également une exponentielle complexe de même fréquence, mais modulée par un facteur de gain complexe. Cette propriété fondamentale, en lien avec des outils de décomposition comme la décomposition en exponentielles complexes pour les sinusoïdes (via les formules d'Euler) ou la décomposition en série de Fourier pour les signaux périodiques, permet de comprendre simplement l'effet d'un système SLIT sur différents types de signaux d'entrée.

Exponentielle Complexe

Lorsque l'entrée est une exponentielle complexe de pulsation $\omega$, c'est-à-dire $x(t)=e^{j\omega t}u(t)$, la solution particulière s'exprime sous la forme

$$y_p(t)=H(j\omega )e^{j\omega t}$$

• $H(j\omega )$ correspond à la fonction de transfert du système évaluée pour $s=j\omega$. Ce terme représente la réponse en fréquence du système, c'est-à-dire le gain complexe (amplitude et phase) que le système applique à l'entrée de pulsation $\omega$.

Démonstration

Lorsque l'entrée s'exprime sous la forme $x(t)=e^{j\omega t}u(t)$, une solution particulière du système s'exprime sous la même forme, c'est-à-dire $y_p(t)=c{e}^{j\omega t}$. Pour déterminer le coefficient $c$, nous remplaçons $x(t)$ et $y_p(t)$ dans l'équation différentielle du système :

$$c{a}_n(j\omega {)}^n{e}^{j\omega t}+\cdots +c{a}_1(j\omega )e^{j\omega t}+c{a}_0{e}^{j\omega t}=b_m(j\omega {)}^m{e}^{j\omega t}+\cdots +b_0{e}^{j\omega t}.$$

En factorisant et en simplifiant, nous obtenons

$$c(a_n(j\omega {)}^n+\cdots +a_1(j\omega )+a_0)=b_m(j\omega {)}^m+\cdots +b_0.$$

Il en résulte que :

$$c=\frac{b_m(j\omega {)}^m+\cdots +b_0}{a_n(j\omega {)}^n+\cdots +a_1(j\omega )+a_0}$$

En identifiant avec la forme de la fonction de transfert, il est finalement possible d'établir que $c=H(j\omega )$.

INFO

Pour tous les systèmes réels ($a_n\in \mathbb{R}$ et $b_m\in \mathbb{R}$), la fonction de transfert respecte la propriété de symétrie hermitienne suivante: $H(j\omega )=H^{\ast }(-j\omega )$. Pour cette raison, il est courant de ne représenter la réponse fréquentielle que pour les pulsations positives $\omega >0$.

Sinusoïde

Lorsque l'entrée du système est une sinusoïde de pulsation $\omega$, c'est-à-dire $x(t)=E\cos (\omega t+{\phi }_e)u(t)$, la solution particulière est également une sinusoïde de même pulsation et s'exprime sous la forme

$$y_p(t)=E|H(j\omega )|\cos (\omega t+{\phi }_e+\arg [H(j\omega )])$$

• $|H(j\omega )|$ correspond à l'amplification (ou au gain) du système à la pulsation $\omega$,
• $\arg [H(j\omega )]$ correspond au déphasage du système à la pulsation $\omega$.

Démonstration

La sinusoïde d'entrée peut se décomposer sous la forme de deux exponentielles complexes via la formule d'Euler :

$$x(t)=E\cos (\omega t+{\phi }_e)=\frac{E}{2}(e^{j(\omega t+{\phi }_e)}+e^{-j(\omega t+{\phi }_e)})u(t).$$

• Pour le terme $e^{j\omega t}$, la solution particulière est :

$$y_{+}(t)=\frac{E}{2}H(j\omega )e^{j(\omega t+{\phi }_e)}.$$

• Pour le terme $e^{-j\omega t}$, la solution particulière est :

$$y_{-}(t)=\frac{E}{2}H(-j\omega )e^{-j(\omega t+{\phi }_e)}.$$

En exploitant le fait que $H(-j\omega )=H^{\ast }(j\omega )$, nous obtenons

$$y_p(t)=y_{+}(t)+y_{-}(t)=\frac{E}{2}(H(j\omega )e^{j(\omega t+{\phi }_e)}+{(H(j\omega )e^{j(\omega t+{\phi }_e)})}^{\ast })$$

Il en vient que :

$$y_p(t)=E\text{Re}(H(j\omega )e^{j(\omega t+{\phi }_e)})$$

et donc

$$y_p(t)=E|H(j\omega )|\cos (\omega t+{\phi }_e+\arg [H(j\omega )]).$$

Diagramme de Bode

Le diagramme de Bode présente graphiquement :

• l'évolution de $|H(j\omega )|$ en fonction de $\omega$ (ou de la fréquence). Cette courbe est généralement représentée en utilisant des échelles logarithmiques pour le module et la pulsation
• l'évolution de $\arg [H(j\omega )]$ en fonction de $\omega$. Cette courbe est généralement représentée en degrés pour l'argument et en échelle logarithmique pour la pulsation.

Cette représentation permet de caractériser le comportement du système pour les différentes fréquences qui constituent le signal d'entrée. Le plus souvent, les axes des abscisses et des ordonnées sont représentés en échelle logarithmique pour mieux mettre en évidence certaines propriétés du système.

TIP

Dans le domaine fréquentiel, le gain statique peut être évalué en calculant $H(j0)$.

Exemple

La figure suivante présente le diagramme de Bode d'un filtre de second ordre.

Diagramme de Bode

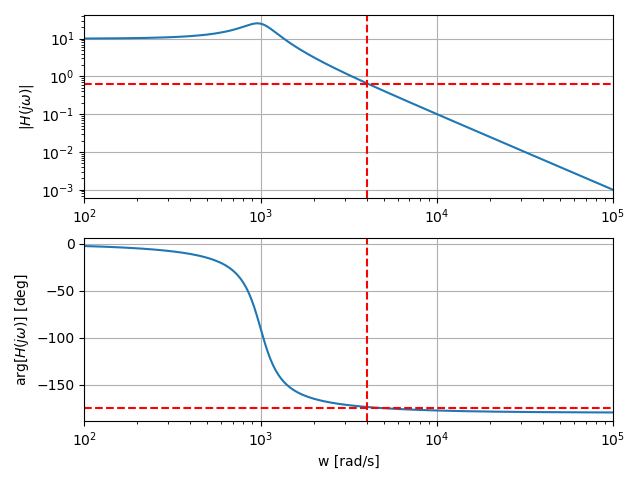
Le gain et le déphasage à la pulsation $\omega =4000$ rad/s sont représentés par les droites en pointillé. Pour cette même pulsation, la figure ci-dessous présente la sinusoïde en entrée et à la sortie du système. On observe bien une amplification d'environ $0.7$ et un déphasage proche de $180$ degrés.

Réponse du système