Synthèse des Filtres d'ordre N

La réalisation d'un filtre est souvent motivée par des contraintes fréquentielles. On peut souhaiter supprimer une bande fréquentielle particulière ou au contraire ne laisser passer que cette bande. En analogique, il est impossible d'imposer des contraintes "dures" (on laisse passer ou on ne laisse pas passer), on utilisera le plus souvent des contraintes "douces" spécifiées par le gabarit fréquentiel. Pour réaliser un filtre compatible avec le gabarit fréquentiel, l'ordre 1 ou 2 sera fréquemment insuffisant et nous aurons généralement recours à des filtres d'ordre N.

Cahier des charges

Filtres idéaux

Lorsque l'on souhaite synthétiser un filtre, la cahier des charges stipule différentes contraintes.

Caractérisation du module

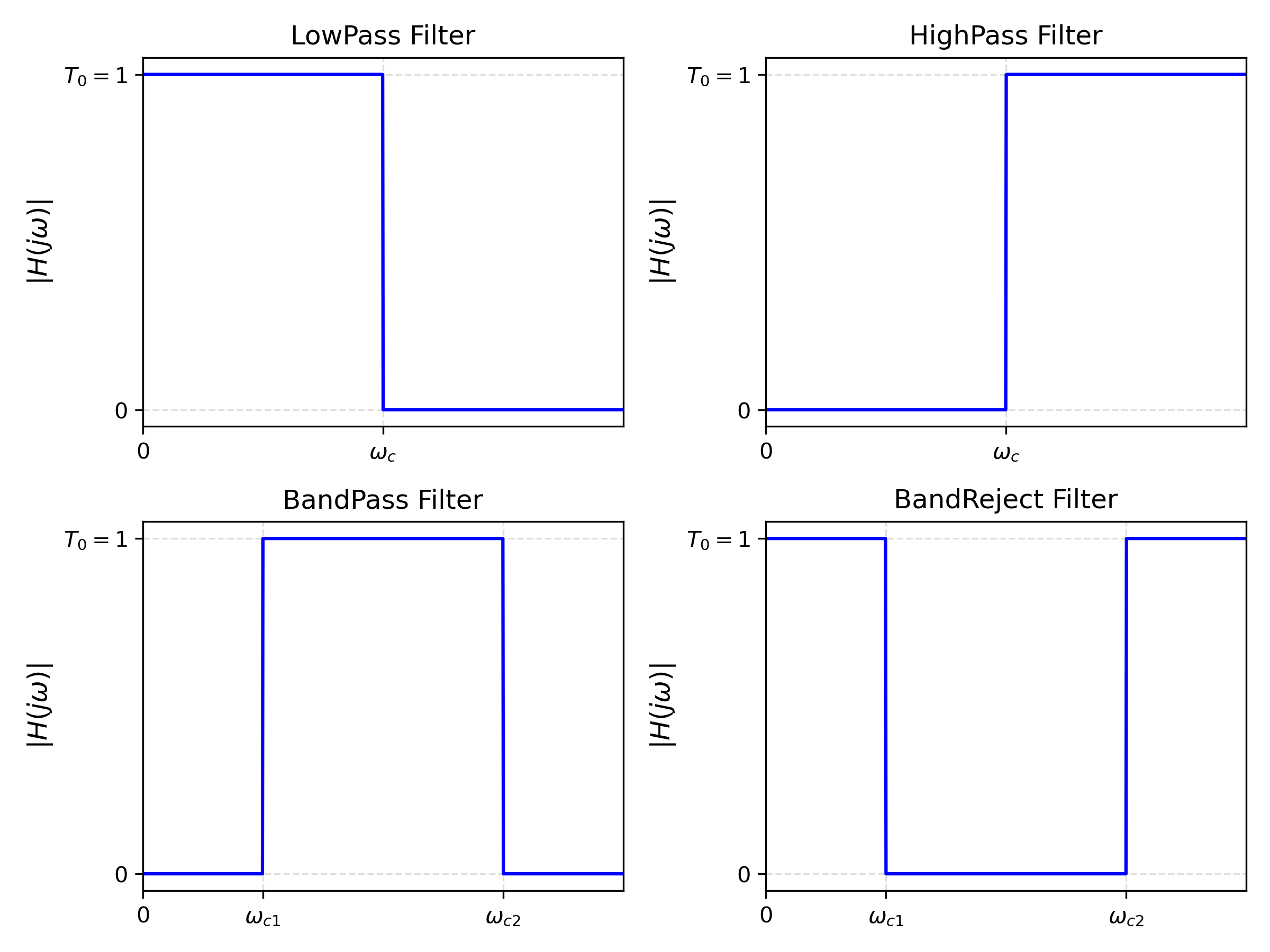
• Filtre en mur de briques (tout ou rien): Module constant dans une bande passante $\mathcal{I}$, c-à-d

$$|H(j\omega )|=\{\begin{array}{cc}1& \text{ si }\omega \in \mathcal{I}\\ 0& \text{ailleurs}\end{array}$$

Filtres Idéaux: Module en mur de briques

Caractérisation de la phase

• Filtre à phase linéaire dans la bande passante c-à-d :

$$\arg [H(j\omega )]=-\omega \tau$$

où $\tau$ désigne le retard de phase.

INFO

La linéarité de la phase dans la bande passante permet d'éviter de déformer le signal dans la bande passante (toutes les composantes sont retardées uniformément).

Filtres Réels

En pratique, il ne sera pas possible de respecter ces contraintes "dures" avec un filtre réel. Dans ce contexte, il est courant de recourir à des contraintes "douces".

Caractérisation du module

Pour spécifier les contraintes sur le module, une solution possible consiste à imposer un gabarit fréquentiel. Le gabarit est spécifié par plusieurs points singuliers.

Exemple du filtre Passe-Bas

Gabarit d'un filtre passe-bas

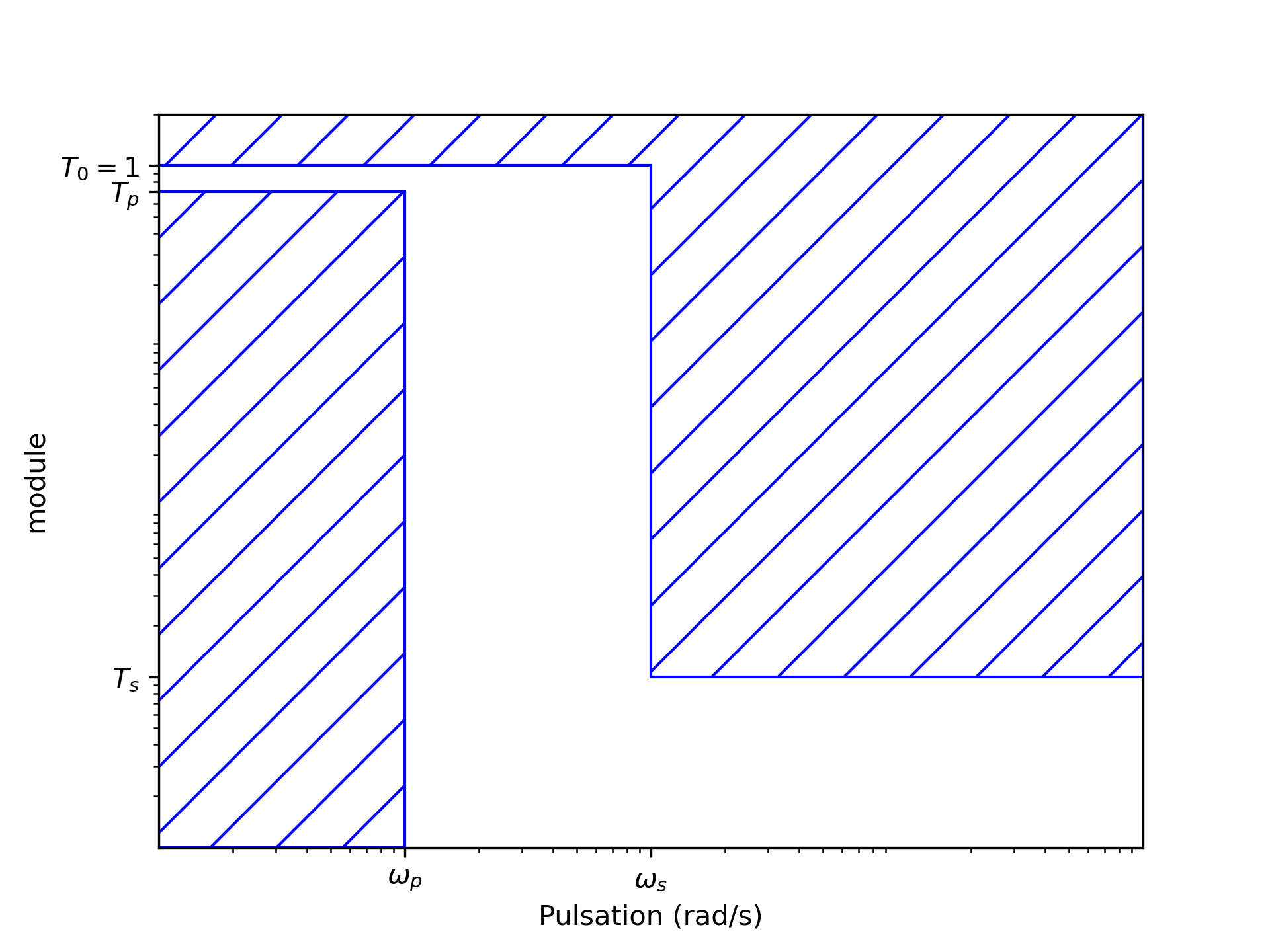
Dans le cas d'un filtre passe-bas, le gabarit est spécifié par les deux points $({\omega }_p,T_p)$ et $({\omega }_s,T_s)$.

• ${\omega }_p$ est la pulsation de coupure (cutoff frequency) et fixe la bande passante (bandwidth) du filtre. Dans la bande passante, on accepte que l’amplification descende au pire à la valeur $T_p$. On tolère parfois une ondulation du module dans la bande passante.

• ${\omega }_s$ fixe le début de la bande atténuée (stop band), pour laquelle le filtre atténue au moins à la valeur $T_s$.

Conversion dB / Valeur Naturelle

L'amplification maximale dans la bande passante est parfois spécifié en valeur naturelle $G_{nat}$ ou en dB $G_{dB}$. Pour passer de l'un à l'autre, il suffit de retenir la relation

$$G_{dB}=20{\log }_{10}(G_{nat})$$

Approximation de l'ordre du filtre

Pour un filtre passe-bas, la spécification du gabarit permet d'obtenir une valeur approchée de l'ordre du filtre. Le comportement asymptotique haute-fréquence d'un filtre passe-bas d'ordre $N$ est donnée par $|H_{HF}(j\omega )|=T_0(\frac{\omega }{{\omega }_0}{)}^{-N}$. En imposant que le comportement asymptotique passe par les deux points singuliers, nous obtenons :

$$N=-\frac{\ln (T_p/T_s)}{\ln ({\omega }_p/{\omega }_s)}$$

Exemple

Le cahier des charges impose $T_0=1$, $T_p=\frac{1}{\sqrt{2}}$, $f_p=1$kHz, $T_s=0.001$ et $f_s=10$kHz. L'ordre approché est alors égal à :

$$N=-\frac{\ln (T_p/T_s)}{\ln (f_p/f_s)}=2.85$$

En pratique, nous utiliserons un filtre d'ordre 3.

Caractérisation de la phase

la phase est rarement linéaire sur l’ensemble des fréquences. On caractérise la non-linéarité de la phase du filtre par son temps de propagation de groupe (group delay) qui est défini par

$$\tau (\omega )=-\frac{d\arg [H(j\omega )]}{d\omega }$$

Cette mesure donne le retard (en secondes) apporté pour chaque pulsation par le filtre. Une phase linéaire impose un retard constant pour chaque fréquence.

Modélisation et Cascade de filtres

Un filtre d'ordre $N$ peut être modélisé par une fonction de transfert exprimée sous la forme polynomiale suivante [modèle ba] :

$$H(s)=\frac{b_N{s}^N+b_{N-1}{s}^{N-1}+\cdots +b_{1}s+b_0}{a_N{s}^N+a_{N-1}{s}^{N-1}+\cdots +a_{1}s+a_0}$$

Cette formulation est cependant mal adaptée à la réalisation pratique de filtres analogique. En effet, un ordre $N$ sera le plus souvent obtenu en cascadant des filtres d'ordre $2$, avec éventuellement un ordre 1 si l'ordre est impair. Dans ce contexte, il est préférable de décomposer la fonction de transfert sous la forme de sections d'ordre 2 [modèle SOS]. Cette décomposition peut s'obtenir à partir de du modèle Pôles et Zéros [modèle zpk]

Modèle Pôles et Zéros (zpk)

Le modèle zpk s'exprime sous la forme :

$$H(s)=k\frac{(s-z_1)\times \cdots (s-z_M)}{(s-p_1)\times \cdots (s-p_N)}$$

où :

• $k$ correspond à un coefficient d'amplification,
• $z_1,\cdots ,z_M$ correspondent aux zéros de la fonction de transfert,
• $p_1,\cdots ,p_N$ correspondent aux pôles de la fonction de transfert.

Modèle SOS (Second Order Sections)

$$H(s)=\prod _{m=1}^{N/2}\left(\frac{b_{2m}{s}^2+b_{1m}s+b_{0m}}{a_{2m}{s}^2+a_{1m}s+a_{0m}}\right)$$

Pour obtenir les paramètres d'un modèle SOS, une approche possible consiste à exploiter le modèle poles et zéros (zpk). En regroupant les pôles par paires de pôles complexes-conjugués, il est possible d'obtenir une cascade de cellules d'ordre 2. Lorsque les cellules d'ordre 2 sont identifiés, il est possible d'implémenter le filtre sur un circuit de type Rauch ou Sallen-Key.

Exemple

Considérons un filtre d'ordre $4$ avec une fonction de transfert exprimée sous la forme polynomiale suivante :

$$H(s)=\frac{0.708}{5.650s^4+3.286s^3+6.605s^2+2.287s+1}$$

Ce filtre possède :

• aucun zéro $z=\{.\}$,
• 4 pôles en $p=\{-0.205+0.392j,-0.085+0.946j,-0.085-0.946j,-0.205-0.392j\}$,
• un facteur de gain $k=0.125$.

En regroupant les paires de pôles complexe-conjugués et en affectant arbitrairement le gain sur la première section, nous pouvons réécrire la fonction de transfert sous la forme:

$$H(s)=\frac{0.125}{s^2+0.41s+0.195}\times \frac{1}{s^2+0.17s+0.903}$$

En passant par les formes normalisées, nous obtenons :

$$H(s)=\frac{0.641}{5.128s^2+2.102s+1}\times \frac{1.107}{1.107s^2+0.188s+1}$$

Pour chaque cellule, il est alors possible d'obtenir la pulsation propre ${\omega }_0$ et le coefficient d'amortissement $m$.

Synthèse de Filtre Passe-Bas Normalisé d'ordre N

Dans cette section, nous allons nous focaliser sur la synthèse d'un filtre passe-bas normalisé ${\omega }_p=1$ rad/s à partir des spécifications du gabarit et de l'estimation $N$ de l'ordre du filtre. Pour synthétiser un filtre d'ordre N, au lieu de déterminer directement les coefficients du modèle ba, il est préférable de déterminer les paramètres du modèles zpk. En effet, ce modèle permet d'obtenir plus efficacement les paramètres du modèle SOS du filtre d'ordre $N$.

1. Filtre de Butterworth

Expression du module

En utilisant la technique de synthèse de Butterworth, le module de la réponse fréquentiel est égal à :

$$|H(j\omega )|=\frac{1}{\sqrt{1+{\omega }^{2N}}}$$

Caractéristiques de la réponse fréquentielle

• Il est possible de montrer que pour les filtres ayant un module monotone, la technique de Butterworth possède la réponse la plus plate dans la bande passante.
• A la pulsation $\omega =1$ rad/s, le module est égal à :

$$|H(1j)|=\frac{1}{\sqrt{2}}$$

Expression de la fonction de transfert

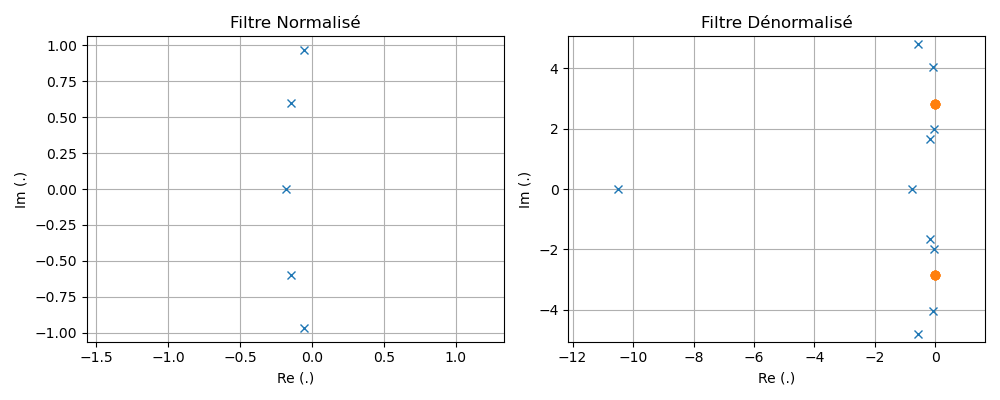
Le modèle zpk de du filtre normalisée s'exprime sous la forme :

$$H(s)=\frac{1}{(s-p_1)\times \cdots (s-p_N)}$$

où

$$p_n=e^{j\pi (2k+N-1)/2N}$$

Cette technique de synthèse place tous les pôles sur un demi-cercle de rayon unitaire (car $|p_n|=1$).

Illustrations

INFO

• Fonction scipy buttap (documentation)

Les figures suivantes présentent respectivement la réponse fréquentielle ainsi que le diagramme des pôles et zéros de plusieurs filtres utilisant la technique de synthèse de Butterworth.

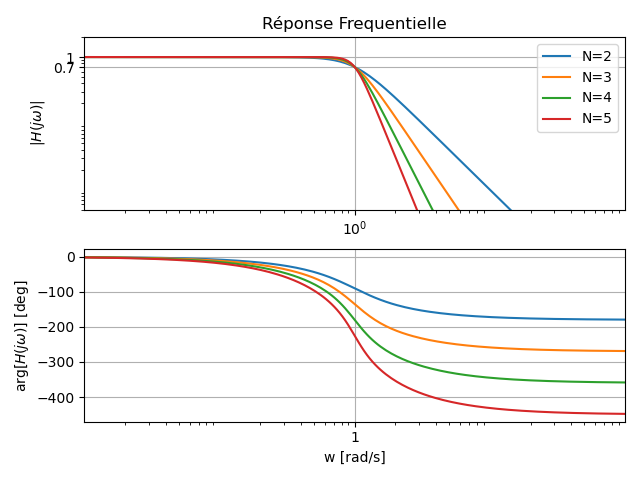
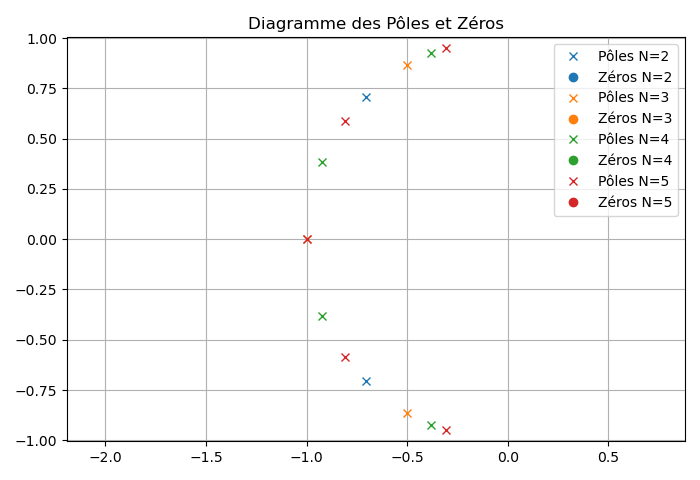
Calibration de $T_p$

La synthèse d’un filtre de Butterworth standard conduit à une réponse en fréquence dont le module, à la fréquence de coupure normalisée $\omega =1$, est fixé à $|H(j1)|=T_p=\frac{1}{\sqrt{2}}$. Il est toutefois possible d’ajuster a posteriori les paramètres zéros-pôles-gain (zpk) de la fonction de transfert pour imposer une amplification minimale différente, c’est-à-dire une valeur désirée de $|H(j1)|=T_p$. Cette calibration de $T_p$ peut être obtenue en modifiant les pôles $p_n$ et le gain $k$ selon :

$$\begin{array}{rl}{p}_n^{\prime }& =\alpha \times p_n\\ k^{\prime }& ={\alpha }^N\times k\end{array}$$

avec

$$\alpha ={\left(\frac{1}{\frac{1}{T_p^2}-1}\right)}^{\frac{1}{2N}}$$

2. Filtre de Chebyshev

Expression du module

En utilisant la technique de synthèse de Chebyshev, le module de la réponse fréquentiel est égal à :

$$|H(j\omega )|=\frac{1}{\sqrt{1+{ϵ}_p^2{T}_n^2(\omega )}}$$

où ${ϵ}_p$ est un paramètre permettant de controller les oscillations dans la bande passante et $T_n(x)$ est le polynôme de Chebyshev d'ordre $n$.

Polynome de Chebychev

Le polynôme de Chebyshev d'ordre $n$ est défini par

$$T_n(x)=\{\begin{array}{cl}\cos (n\arccos (x))& \text{ pour }|x|<1\\ \cosh (n{\cosh }^{-1}(x))& \text{ pour }x\ge 1\\ (-1{)}^n\cosh (n{\cosh }^{-1}(-x))& \text{ pour }x\ge -1\end{array}$$

Caractéristiques de la réponse fréquentielle

• Le module présente une ondulation dans la bande passante.
• Comme $T_n(1)=1$, le module à la pulsation $\omega =1$ rad/s est égal à :

$$|H(1j)|=\frac{1}{\sqrt{1+{ϵ}_p^2}}$$

• Comme $T_{2q+1}(0)=0$ et $T_{2q}(0)=1$ pour $q\in \mathbb{N}$, nous obtenons en basse-fréquences la limite :

$$T_0=|H(0j)|=\{\begin{array}{cl}1& \text{ si }n=2q+1,\\ \frac{1}{\sqrt{1+{ϵ}_p^2}}& \text{ si }n=2q.\end{array}$$

Expression de la fonction de transfert

Le modèle zpk de du filtre normalisée s'exprime sous la forme :

$$H(s)=\frac{k}{(s-p_1)\times \cdots (s-p_N)}$$

avec

$$\begin{array}{rl}{p}_n& =j\cos (\frac{\pi (2n-1)}{2N}-\frac{n}{N}{\sinh }^{-1}\left(\frac{1}{{ϵ}_p}\right))\\ k& =T_0\prod _{n=1}^N(-p_n)\end{array}$$

Il est possible d'établir que tous les pôles sont placés sur une demi-ellipse.

Illustrations

INFO

• Fonction scipy cheb1ap(documentation)

Les figures suivantes présentent respectivement la réponse fréquentielle ainsi que le diagramme des pôles et zéros de plusieurs filtres utilisant la technique de synthèse de Chebychev ($T_c=-3$ dB).

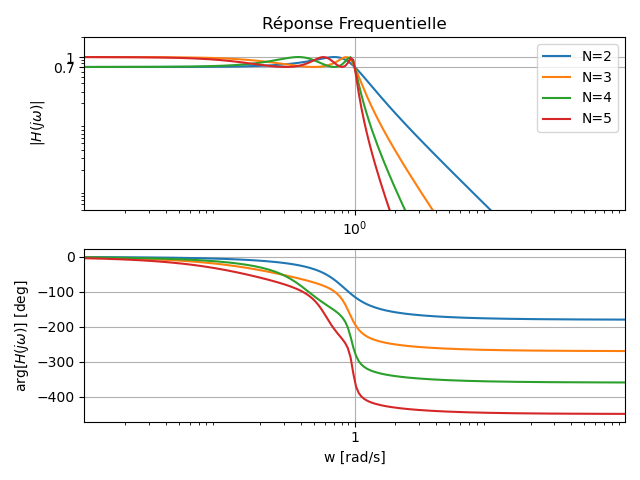
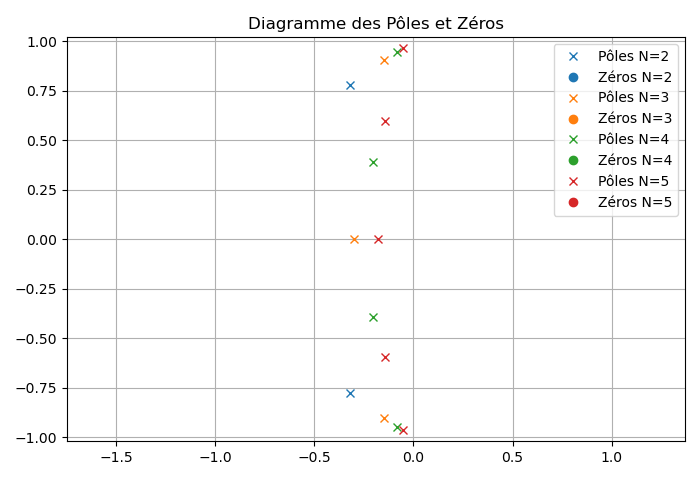
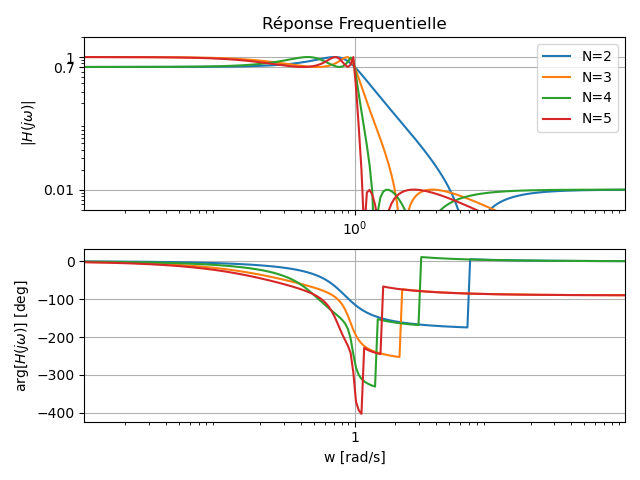
3. Filtre de Cauer (Elliptique)

Expression du module

La technique de synthèse de Cauer permet d'obtenir des filtres normalisés pour lesquels le module est égal à

$$|H(j\omega )|=\frac{1}{\sqrt{1+{ϵ}_p^2{R}_n^2(\omega ,{ϵ}_s)}}$$

où ${ϵ}_p$ est un paramètre permettant de controller les oscillations dans la bande passante, ${ϵ}_s$ est un paramètre permettant de controller les oscillations dans la bande rejetée, et $R_n(x,{ϵ}_s)$ est une fonction elliptique.

Caractéristiques de la réponse fréquentielle

• Le module présente une ondulation dans la bande passante et dans la bande rejetée,
• Le module à la pulsation $\omega =1$ rad/s est égal à :

$$|H(1j)|=\frac{1}{\sqrt{1+{ϵ}_p^2}}$$

• Le gain basse-fréquence est égal à ;

$$T_0=|H(0j)|=\{\begin{array}{cl}1& \text{ si }n=2q+1,\\ \frac{1}{\sqrt{1+{ϵ}_p^2}}& \text{ si }n=2q.\end{array}$$

Expression de la fonction de transfert

Le modèle zpk de du filtre normalisée s'exprime sous la forme :

$$H(s)=k\frac{(s-z_1)\cdots (z-z_{N/2})}{(s-p_1)\times \cdots (s-p_N)}$$

Le filtre présente des zéros positionnés sur l'axe des imaginaires purs. Ces zéros correspondent à des fréquences rejetées.

Illustrations

INFO

• Fonction scipy ellipap (documentation)

Les figures suivantes présentent respectivement la réponse fréquentielle ainsi que le diagramme des pôles et zéros de plusieurs filtres utilisant la technique de synthèse de Cauer ($T_c=-3$ dB, $T_s=-40$ dB).

4. Filtre de Bessel

Expression de la fonction de transfert

En utilisant la technique de synthèse de Bessel, la fonction de transfert d'un filtre normalisé d'ordre N s'exprime sous la forme :

$$H(s)=\frac{k}{B_n(s)}$$

où $B_n(s)$ correspond à un polynôme de Bessel d'ordre $N$.

Polynôme de Bessel

Le polynôme de Bessel s'obtient à partir de la relation de récurrence suivante :

$$B_n(x)=(2n+1)B_{n-1}(x)+x^2{B}_{n-2}(x)$$

avec

• $B_0(x)=1$,
• $B_1(x)=1+x$.

Cette fonction de transfert peut s'exprimer sous la forme zpk suivante :

$$H(s)=\frac{k}{\prod _{n=1}^{N}s-p_n}$$

avec $k=\prod _{n=1}^N-p_n=B_n(0)$. Notons qu'il n'y a pas de formule simple pour obtenir les pôles de la fonction de transfert. Les pôles sont généralement obtenus numériquement. A titre d'exemple, le tableau suivant présente la valeur des pôles pour $n=2,3,4,5$.

n	pôles
2	-1.5 $\pm$ 0.8660j
3	-2.32219, -1.83891 $\pm$ 1.75438j
4	-2.10379 $\pm$ 2.65742j, -2.89621 $\pm$ 0.86723j
5	-3.64674, -2.32467 $\pm$ 3.57102j, -3.35196 $\pm$ 1.74266j

Caractéristiques de la réponse fréquentielle

Le filtre de Bessel possède les propriétés suivantes :

• Le gain statique est unitaire c-à-d $T_0=|H(0j)|=1$,
• La réponse fréquentielle est quasi-linéaire dans la bande passante.

Illustrations

INFO

• Fonction scipy besselap (documentation)

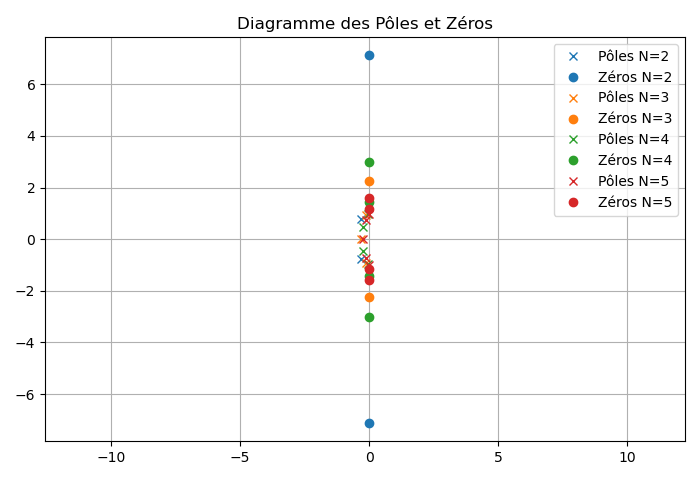
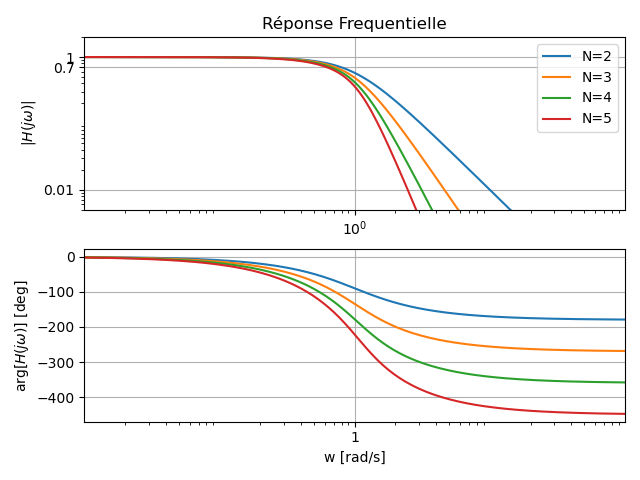
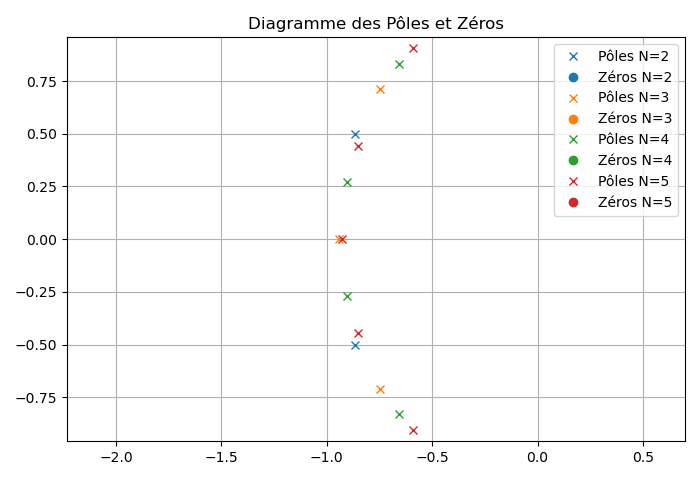
Les figures suivantes présentent respectivement la réponse fréquentielle ainsi que le diagramme des pôles et zéros de plusieurs filtres utilisant la technique de synthèse de Bessel.

Méthodologie de réalisation d’un filtre d’ordre $N$

Pour synthétiser des filtres quelconques, il faut transformer la variable $s$ de manière à retomber systématiquement sur la synthèse d’un filtre passe-bas de pulsation de coupure normalisée ${\omega }_{p,lp}=1$. L’application de la transformation inverse permet ensuite de réaliser la synthèse du filtre d'origine.

La méthodologie de conception de filtre d'ordre $N$ est alors composée de plusieurs étapes.

Obtention du gabarit passe-bas normalisé

La fonction de transfert d'un filtre $H(s)$, quelque soit son type, peut s'obtenir en construisant son équivalent passe-bas normalisé, $H(s_{lp})$, en utilisant la transformation de la variable de Laplace $s_{lp}=f(s)$ où $f(.)$ est la fonction de transformation. La normalisation doit permettre d'obtenir une pulsation ${\omega }_{p,lp}=1$.

Passe-Bas

La fonction de transformation est donnée par :

$$s_{lp}=\frac{s}{{\omega }_c}$$

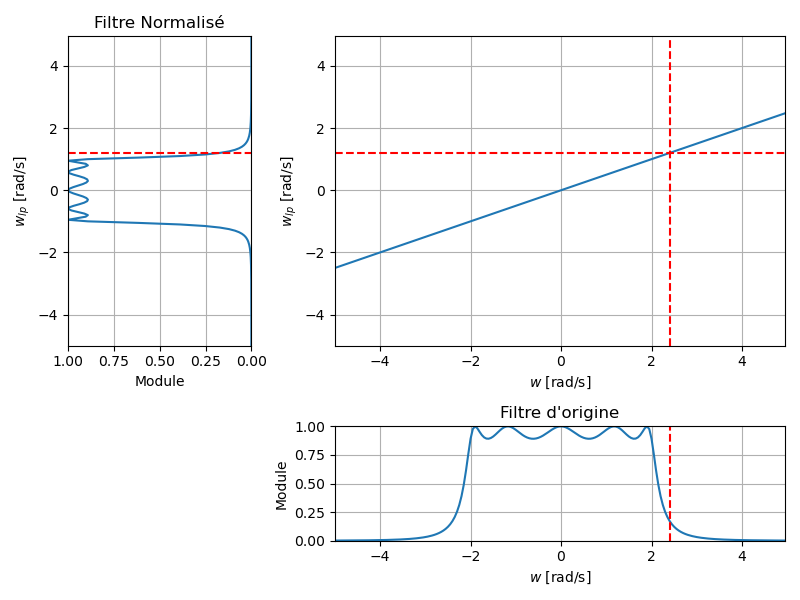
Mapping Fréquentiel

Après transformation, la pulsation $\omega$ rad/s du filtre d'origine est mappée à la pulsation :

$${\omega }_{lp}=\frac{\omega }{{\omega }_c}$$

Passe-Haut

La fonction de transformation est donnée par :

$$s_{lp}=\frac{{\omega }_c}{s}$$

Mapping Fréquentiel

Après transformation, la pulsation $\omega$ du filtre normalisé est mappée à la pulsation

$${\omega }_{lp}=-\frac{{\omega }_c}{\omega }$$

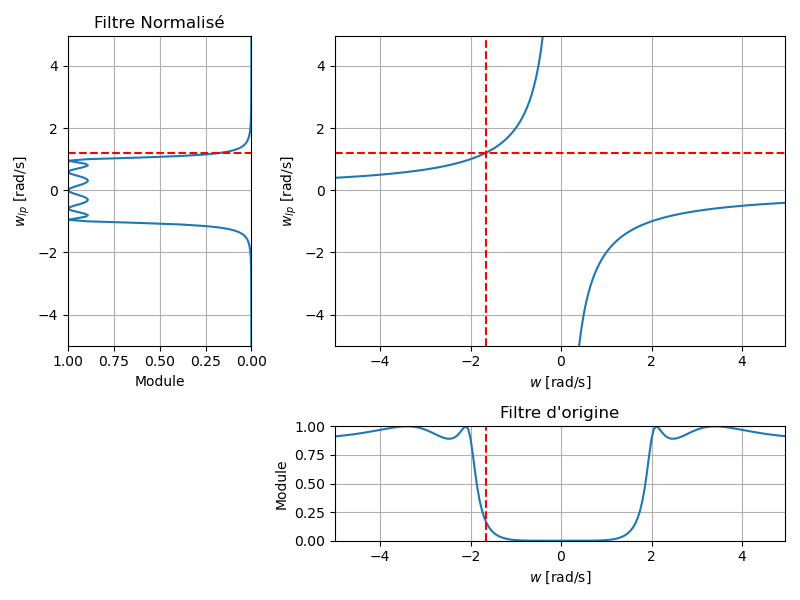
Passe-Bande

La fonction de transformation est donnée par :

$$s_{lp}=\frac{s^2+{\omega }_0^2}{s{\mathrm{\Delta }}_{\omega }}$$

• ${\omega }_0=\sqrt{{\omega }_{c1}{\omega }_{c2}}$,
• ${\mathrm{\Delta }}_{\omega }={\omega }_{c2}-{\omega }_{c1}$ désigne la largeur de la bande passante.

Mapping Fréquentiel

Après transformation, la pulsation $\omega$ du filtre normalisé est mappée à la pulsation :

$${\omega }_{lp}=\frac{{\omega }^2-{\omega }_0^2}{\omega {\mathrm{\Delta }}_{\omega }}$$

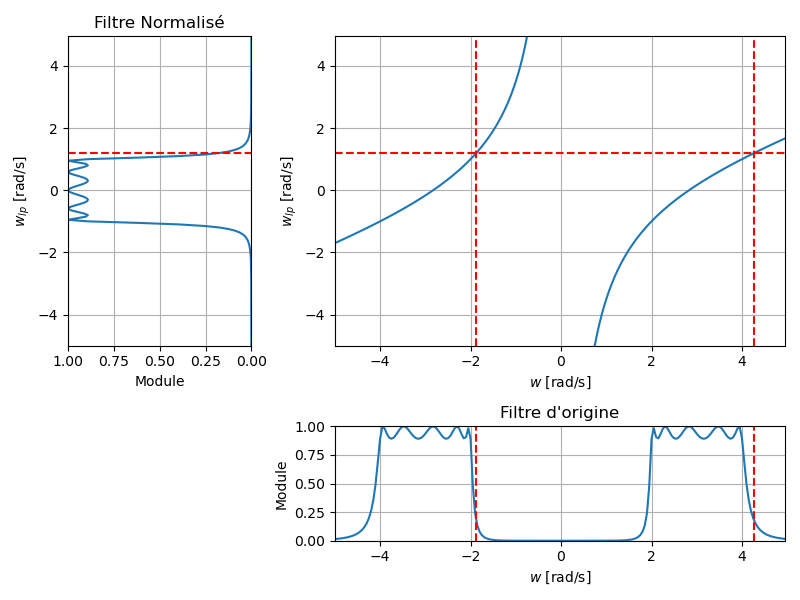
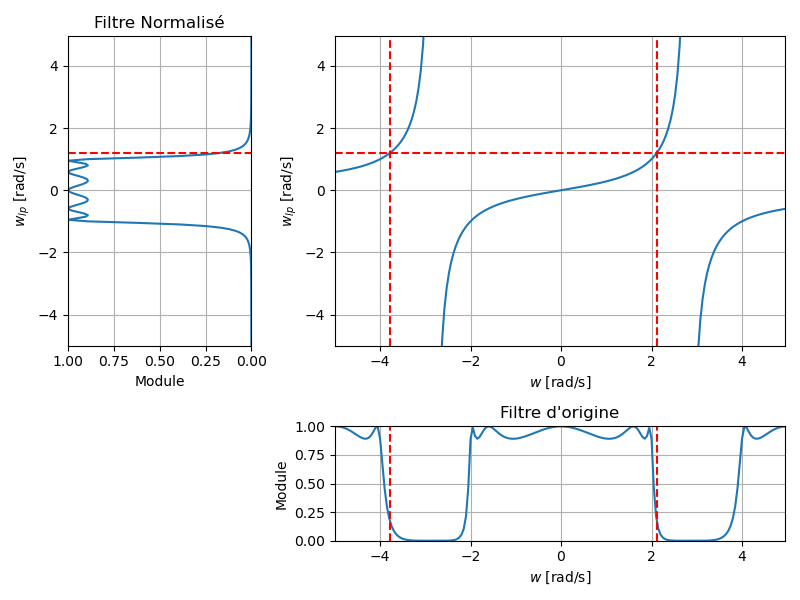
Rejecteur

La fonction de transformation est donnée par :

$$s_{lp}=\frac{s{\mathrm{\Delta }}_{\omega }}{s^2+{\omega }_0^2}$$

• ${\omega }_0=\sqrt{{\omega }_{c1}{\omega }_{c2}}$
• ${\mathrm{\Delta }}_{\omega }={\omega }_{c2}-{\omega }_{c1}$ désigne la largeur de la bande passante.

Mapping Fréquentiel

Après transformation, la pulsation $\omega$ du filtre normalisé est mappée à la pulsation

$${\omega }_{lp}=\frac{\omega {\mathrm{\Delta }}_{\omega }}{{\omega }_0^2-{\omega }^2}$$

Synthèse du filtre Passe-Bas

Utilisation d'une technique de synthèse particulière pour synthétiser le filtre passe-bas (Butterworth, Chebychev, Cauer ou Bessel) normalisé d'ordre $N$. Cette étape de synthèse permet d'obtenir les paramètres du modèle zpk:

$$H_{lp}(s)=k_{lp}\frac{(s-z_{lp,1})\times \cdots (s-z_{lp,M})}{(s-p_{lp,1})\times \cdots (s-p_{lp,N})}$$

où :

• $k_{lp}$ correspond à un coefficient d'amplification,
• $z_{1,lp},\cdots ,z_{M,lp}$ correspondent aux zéros de la fonction de transfert,
• $p_{1,lp},\cdots ,p_{N,lp}$ correspondent aux pôles de la fonction de transfert.

Dénormalisation du filtre passe-bas

Après synthèse du filtre passe-bas, l'étape de dénormalisation s'obtient en modifiant la valeur du gain, des pôles et des zéros. Cette modification dépend du type de filtre.

Vers Passe-Bas

$$\begin{array}{rl}k& =k_{lp}^{N-M}\\ p_n& ={\omega }_p\times p_{lp,n}\\ z_m& ={\omega }_p\times z_{lp,m}\end{array}$$

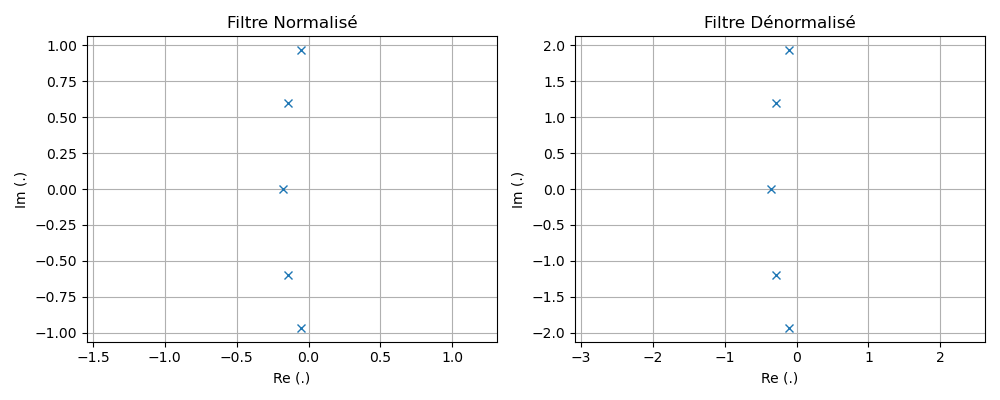
Vers Passe-Haut

$$\begin{array}{rl}k& =1\\ p_n& ={\omega }_p/p_{lp,n}\\ z_m& ={\omega }_p/z_{lp,m}\end{array}$$

Pour obtenir un filtre passe-haut, il est également nécessaire d'ajouter N-M zéros en zéros.

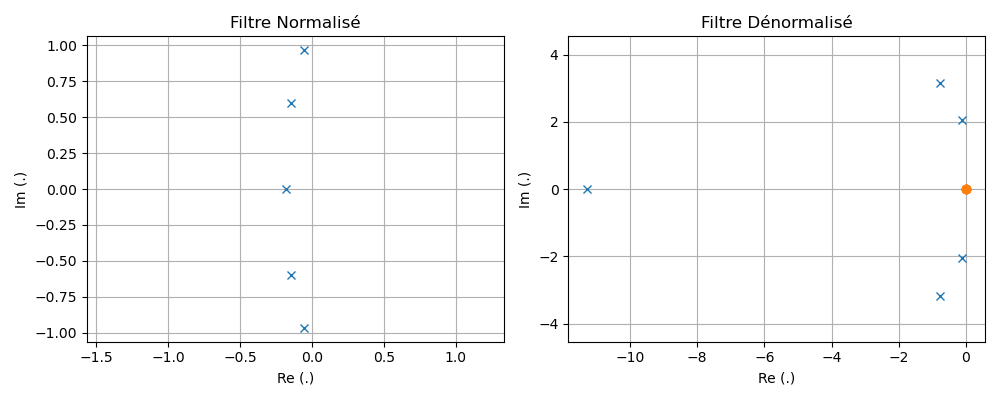
Vers Passe-Bande

$$\begin{array}{rl}k& =k_{lp}(\mathrm{\Delta }\omega {)}^{N-M}\\ \{p_n,p_{2n}\}& =\alpha \times p_{lp,n}\pm \sqrt{{\alpha }^2\times p_{lp,n}^2-{\omega }_0^2}\\ \{z_m,z_{2m}\}& =\alpha \times z_{lp,m}\pm \sqrt{{\alpha }^2\times z_{lp,m}^2-{\omega }_0^2}\end{array}$$

où $\alpha =\mathrm{\Delta }\omega /2$. Pour obtenir un filtre passe-bande, il est également nécessaire d'ajouter $N$ zéros en 0.

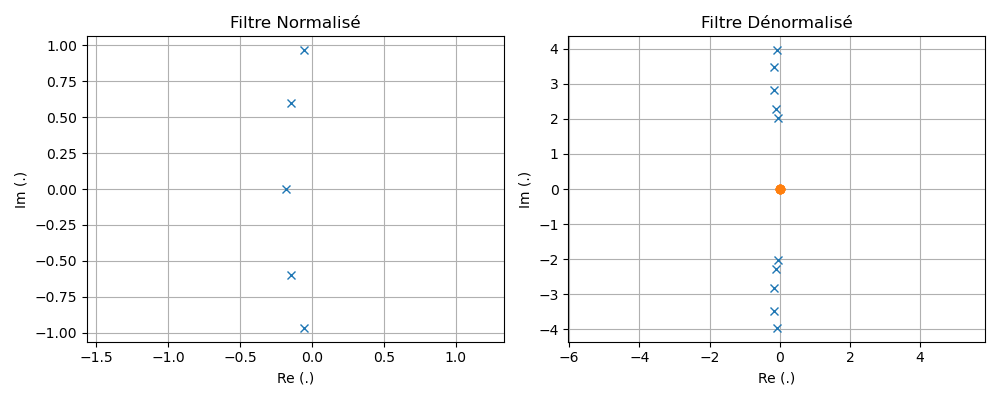
Vers Rejecteur

$$\begin{array}{rl}k& =1\\ \{p_n,p_{2n}\}& =\alpha \times p_{lp,n}^{-1}\pm \sqrt{{\alpha }^2\times p_{lp,n}^{-2}-{\omega }_0^2}\\ \{z_m,z_{2m}\}& =\alpha \times z_{lp,m}^{-1}\pm \sqrt{{\alpha }^2\times z_{lp,m}^{-2}-{\omega }_0^2}\end{array}$$

où $\alpha =\mathrm{\Delta }\omega /2$. Pour obtenir un filtre rejecteur, il est également nécessaire d'ajouter $N$ zéros en $\pm j{\omega }_0$.