Systèmes d'Ordre 1 et 2
Systèmes de Premier Ordre
Modélisation
Équation différentielle
L'équation différentielle d'un système de premier ordre peut s'exprimer sous la forme suivante :
désigne la constante de temps [s].
Fonction de transfert
La fonction de transfert d'un système de premier ordre peut s'exprimer sous la forme normalisée suivante :
désigne le numérateur de la fonction de transfert (polynôme de degré inférieur ou égal à 1).
Expression du pôle
Un système de premier ordre possède un unique pôle. Ce pôle s'obtient en cherchant l'unique racine du dénominateur de la fonction de transfert.
Exemples de circuits
Filtre RC Passe-Bas
Circuit : Résistance
avec
Filtre RC Passe-Haut
Circuit : Condensateur
avec
Réponse Temporelle
La solution complète de l'équation différentielle s'exprime sous la forme :
: solution libre (régime libre)
: solution particulière (régime forcé). L'expression du régime forcé dépend de l'allure de l'entrée et des coefficients et
Exemple : Réponse indicielle d'un passe-bas
Considérons la réponse d'un système de premier ordre à un échelon d'amplitude
La constante d'intégration s'obtient en déterminant une condition initiale. En intégrant l'équation différentielle entre
Pour un filtre passe-bas de premier ordre, la réponse du système à un échelon d'amplitude
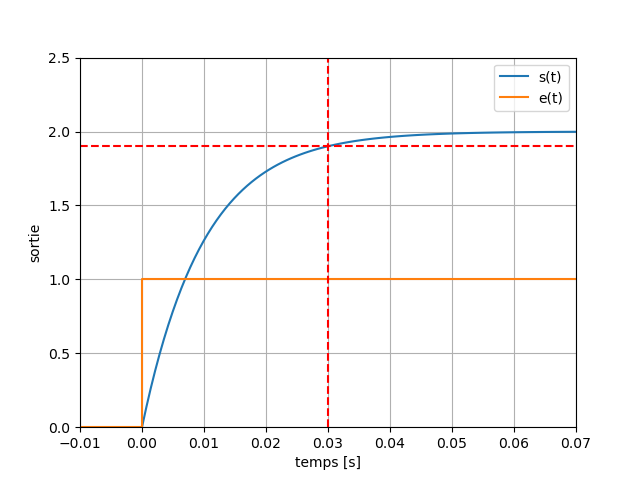
Valeurs Remarquables
- Valeur initiale :
, - Valeur finale :
, - Valeur maximale:
, - Temps de réponse à
: .
Réponse Fréquentielle
La réponse fréquentielle s'obtient en posant
désigne la pulsation de coupure à -3dB [rad/s].
Passe-Bas
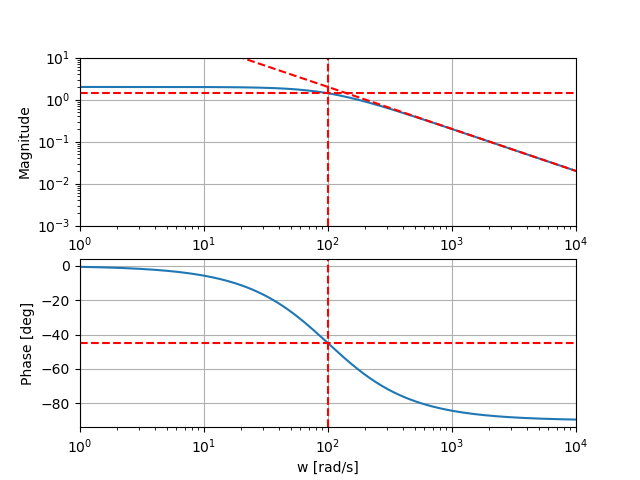
- Module :
- Argument :
Passe-Haut
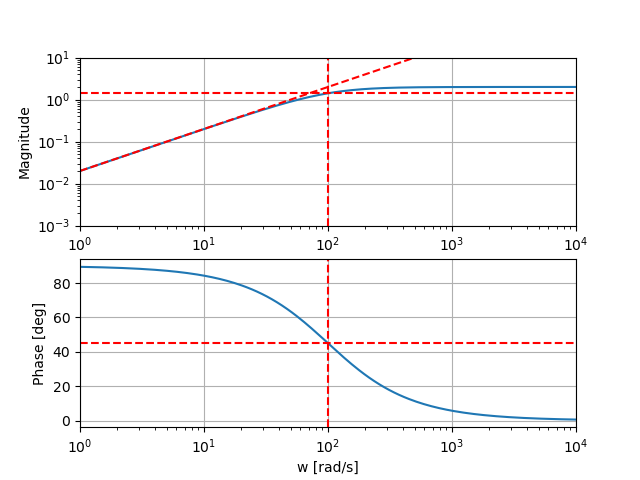
- Module :
- Argument :
Systèmes de Second Ordre
Modélisation du système
Équation différentielle
L'équation différentielle d'un système de second ordre peut s'exprimer sous la forme suivante :
désigne la pulsation propre [rad/s], désigne le coefficient d'amortissement, désigne le facteur de qualité.
Fonction de transfert
La fonction de transfert d'un système de second ordre peut s'exprimer sous la forme normalisée suivante :
désigne le numérateur de la fonction de transfert (polynôme de degré inférieur ou égal à 2).
Exemples de circuits
Les 4 exemples ci-dessous présentent les fonctions de transfert normalisées (
Passe-bas (LP)
Exemple de circuit : Filtre RLC série ou structure Sallen-Key passe-bas.
Passe-bande (BP)
Exemple de circuit : Circuit RLC série avec sortie aux bornes de R.
Passe-haut (HP)
Exemple de circuit : Structure Sallen-Key passe-haut.
Réjecteur (BR)
Exemple de circuit : Circuit bouchon RLC.
Analyse du système
Expressions des Pôles
Les pôles s'obtiennent en déterminant les racines du dénominateur de la fonction de transfert c-à-d en déterminant les valeurs de
Cette équation est une équation du second degré. Le discriminant s'exprime sous la forme suivante:
L'expression du discriminant montre que la valeur de
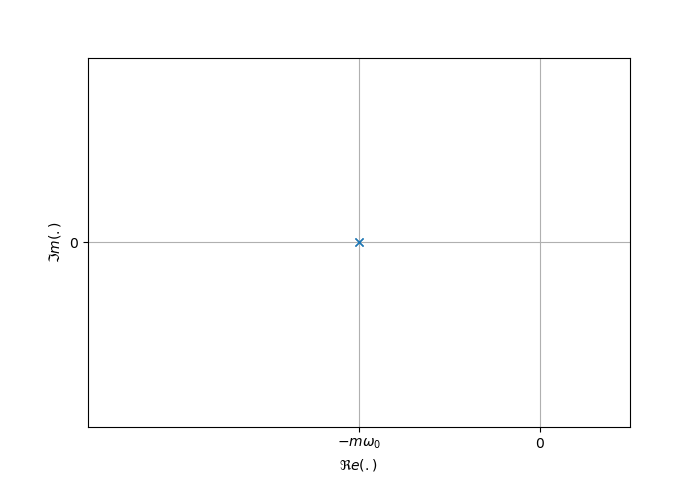
Cas où m>1
Lorsque
Mathématiquement, les deux pôles possèdent les propriétés suivantes:
- le produit des deux pôles est égal à
- la somme des deux pôles est égale à
.
En utilisant ces 2 propriétés, il est possible d'identifier le coefficient d'amortissement et la pulsation propre via les relations :
Géométriquement, les deux pôles sont placés sur un cercle de centre
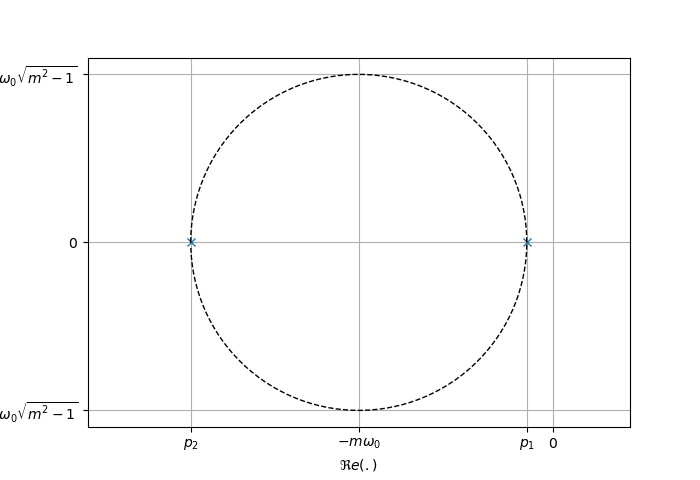
Cas où m=1
Lorsque
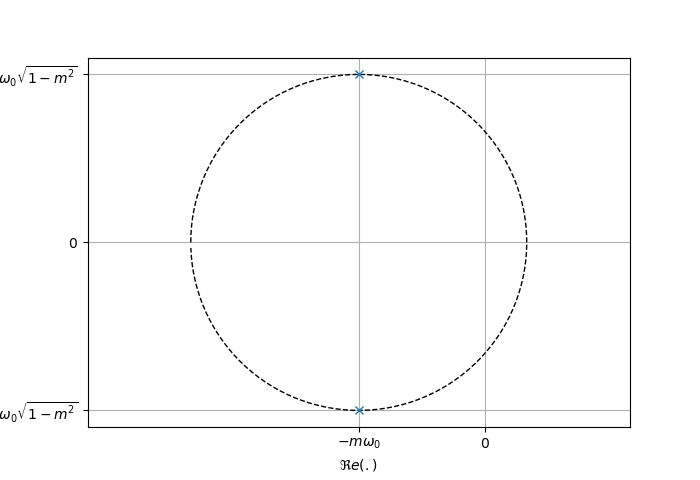
Cas où m<1
Lorsque
Mathématiquement, il est possible de démontrer que :
- le module de chaque pôle est égal à
. - l'angle formé entre le pôle
et l'axe des réels est donné par
En utilisant ces 2 propriétés, il est possible d'identifier le coefficient d'amortissement et la pulsation propre via les relations :
Équation Différentielle et Réponse Temporelle
En utilisant l'équation différentielle, la réponse à une entrée quelconque s'exprime sous la forme :
: solution libre, : solution particulière.
Cas où m>1
La solution libre s'exprime sous la forme :
Nous constatons que la solution libre est donnée par la contribution de deux systèmes de premier ordre ayant pour constantes de temps respectives:
Cas où m<1
La solution libre s'exprime sous la forme d'une sinusoïde amortie:
régit la vitesse de décroissance de l'enveloppe, correspond à la pseudo-pulsation des oscillations [rad/s]
Démonstration
Lorsque
où
Cette expression peut également se simplifier en utilisant la décomposition sous forme polaire de la constante d'intégration et la décomposition sous forme algébrique de
En utilisant l'expression de
Propriétés
- Oscillations : pseudo-pulsation et pseudo-période.
- Ratio des amplitudes après une oscillation :
Lorsque
Cas de la Réponse Indicielle
La réponse indicielle correspond à la réponse du système lorsque l'entrée est un échelon d'amplitude
L'expression de la sortie peut s'obtenir en utilisant l'équation différentielle ou la transformée de Laplace inverse. Spécifiquement, il est possible d'établir que la transformée de Laplace de la sortie est égale à
Valeurs limites en
Concernant les valeurs aux limites, il est possible d'obtenir rapidement le comportement en
- Valeur finale: La valeur finale est donnée par
Valeur initiale. Pour la valeur initiale, nous nous intéressons à la fois à la valeur initiale de
et sa dérivée . Concernant
, nous obtenons : Concernant la dérivée de
, nous obtenons
Cas du passe-haut
Dans le cas du passe-haut, la valeur de la limite de
Cette limite converge vers une valeur finie.
Réponse Fréquentielle
La réponse fréquentielle du système s'obtient en posant
- Expression à la pulsation propre. À la pulsation propre
[rad/s], la réponse fréquentielle s'exprime simplement sous la forme :
Expression du module
Le module s'exprime sous la forme générale suivante :
où
Expression de l'argument
Pour éviter les changements de cadrants liés à l'utilisation de la fonction arctangente, une pré-étape consiste à décomposer la fonction de transfert sous une forme plus simple à manipuler. Spécifiquement, une approche possible consiste à normaliser la partie réelle au dénominateur à 1 pour éviter les indéterminations de phase de la fonction arctangente. En utilisant cette normalisation, nous obtenons :
où
Démonstration
En décomposant la fonction de transfert sous la forme suivante :
Le deuxième terme possède un dénominateur avec une partie réelle positive (pas de changement de cadrant). Nous obtenons alors
Formes Normalisées
Passe-bas (LP)
- gain statique:
, - pulsation propre:
(rad/s), - coefficient d'amortissement:
.
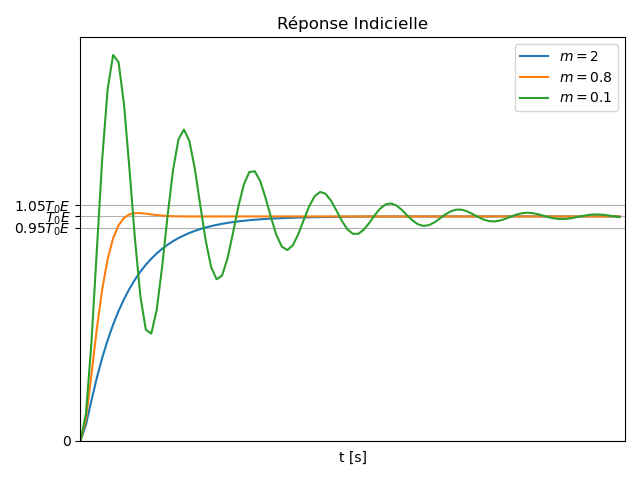
Réponse Indicielle
Expression
- Lorsque
, la réponse indicielle s'exprime sous la forme :
où
- Lorsque
, la réponse indicielle s'exprime sous la forme :
Valeurs Limites
- Valeur initiale:
et . - Valeur finale:
Dépassement (si
Lorsque
Démonstration
Pour obtenir la position des extrema lorsque
Cette dérivée s'annule lorsque
Il est important de pouvoir quantifier la valeur maximale de la réponse indicielle. En pratique, nous utilisons le plus souvent le premier dépassement relatif qui est une grandeur indépendante de
La valeur du premier dépassement peut s'obtenir rapidement en utilisant une abaque présentant
Temps de réponse
Dans certaines applications, il est nécessaire de quantifier la rapidité du système au moyen du temps de réponse à
Il est possible de démontrer que ce temps de réponse dépend uniquement de la pulsation propre
Comportement Fréquentiel
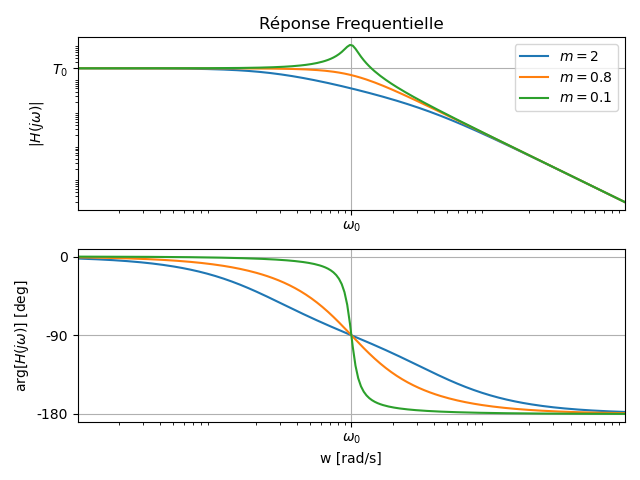
Point singulier et comportements asymptotiques
- Asymptote basse-fréquences:
, - Asymptote haute-fréquences:
, - Valeur à la pulsation propre:
Phénomène de résonance
Si
À la pulsation de résonance, le module est égal à
Passe-bande (BP)
- gain maximum:
, - pulsation propre:
(rad/s), - coefficient d'amortissement:
.
Réponse Indicielle
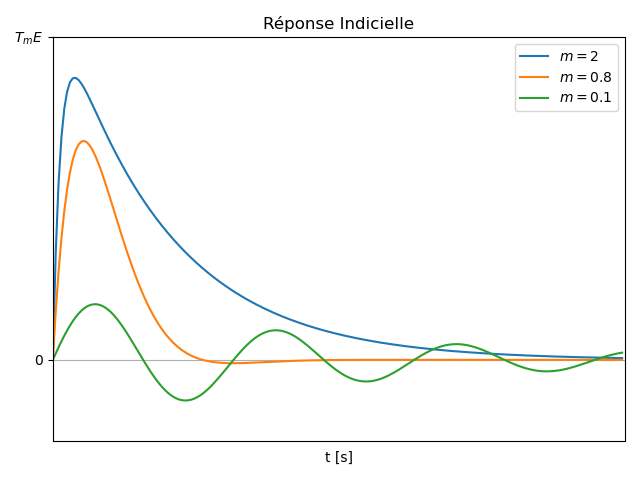
Valeurs Limites
- Valeur initiale:
et . - Valeur finale:
Comportement Fréquentiel
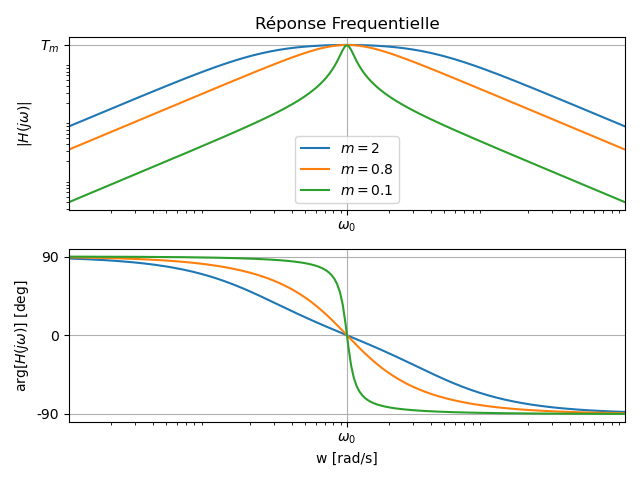
Point singulier et comportements asymptotiques
- Asymptote basse-fréquences:
, - Asymptote haute-fréquences:
, - Intersection des asymptotes de module en
: - Valeur à la pulsation propre:
Pulsation de coupure à -3dB et bande passante
- Pulsation de coupure. Le filtre passe-bande possède deux pulsations de coupure à
( ). Ces pulsations s'expriment sous la forme :
- Bande passante à
dB. La bande passante à dB s'exprime sous la forme :
Passe-haut (HP)
- gain haute-fréquence:
, - pulsation propre:
(rad/s), - coefficient d'amortissement:
.
Réponse Indicielle
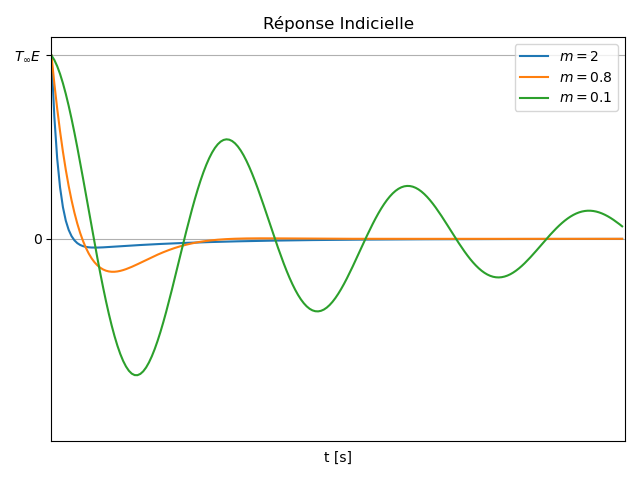
Valeurs Limites
- Valeur initiale:
et . - Valeur finale:
Comportement Fréquentiel
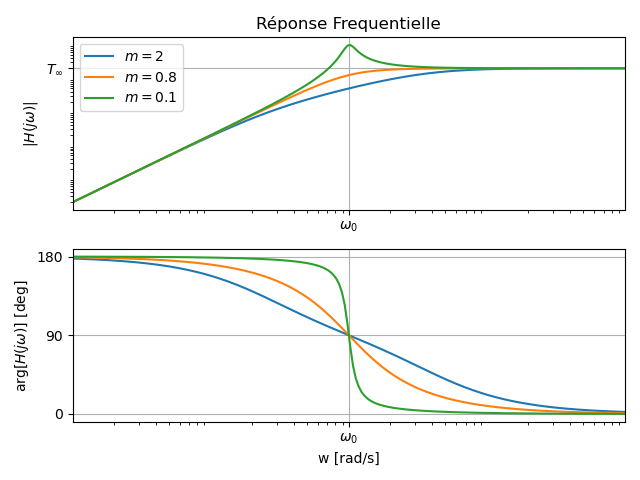
Point singulier et comportements asymptotiques
- Asymptote basse-fréquences:
, - Asymptote haute-fréquences:
, - Valeur à la pulsation propre:
Phénomène de résonance
Si
À la pulsation de résonance, le module est égal à
Réjecteur (Notch)
- gain maximum:
, - pulsation propre:
(rad/s), - coefficient d'amortissement:
.
Réponse Indicielle
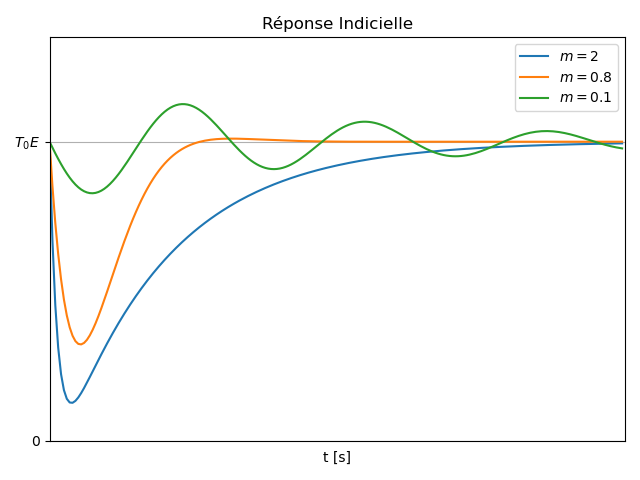
Valeurs Limites
- Valeur initiale:
et . - Valeur finale:
Comportement Fréquentiel
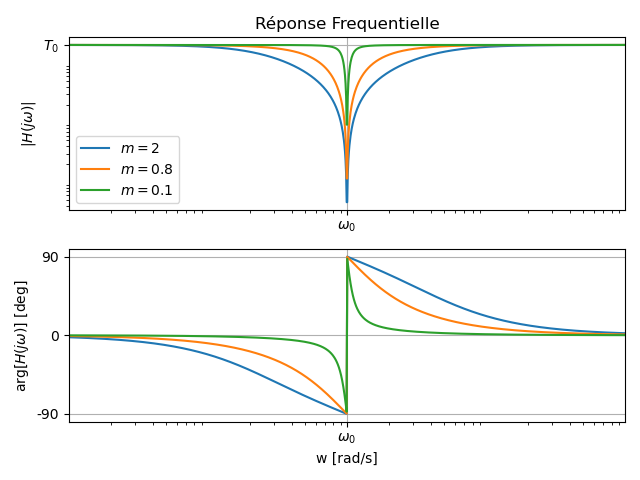
Point singulier et comportements asymptotiques
- Asymptote basse-fréquences:
, - Asymptote haute-fréquences:
, - Valeur à la pulsation propre:
Pulsation de coupure à -3dB et bande rejetée
- Pulsation de coupure. Le filtre réjecteur possède deux pulsations de coupure à
( ). Ces pulsations s'expriment sous la forme :
- Bande rejetée à
dB. La bande rejetée à dB s'exprime sous la forme :
