Caractérisation et Identification

Ce chapitre présente les méthodologies permettant d'identifier les paramètres caractéristiques d'un système SLIT à partir de différentes représentations : diagramme des pôles et zéros, réponse indicielle ou réponse fréquentielle.

Objectifs de la caractérisation

La caractérisation d'un système consiste à déterminer ses propriétés fondamentales :

Caractéristiques temporelles

• Stabilité : Le système converge-t-il vers un état d'équilibre ?
• Présence de dépassement : La réponse dépasse-t-elle la valeur finale ?
• Temps de réponse à 5% : Temps pour atteindre définitivement ±5% de la valeur finale
• Amortissement : Caractère oscillatoire ou apériodique de la réponse

Caractéristiques fréquentielles

• Type de filtre : Passe-bas, passe-haut, passe-bande, réjecteur
• Amplification : Gain statique ou gain maximum
• Fréquence propre : Fréquence caractéristique du système
• Résonance : Présence et valeur du pic de résonance
• Comportement asymptotique : Pente en basse et haute fréquence

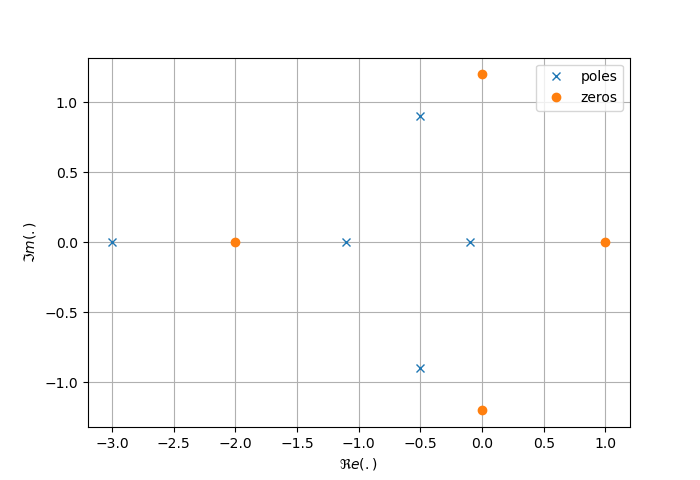
Identification à partir du diagramme des pôles et zéros

Le diagramme des pôles et zéros fournit une représentation visuelle qui permet d'identifier rapidement les caractéristiques principales d'un système.

Stabilité

Un système est asymptotiquement stable si et seulement si tous les pôles sont situés dans le demi-plan gauche du plan complexe, c'est-à-dire :

$$\text{Re}(p_k)<0\text{pour tout }k$$

Exemple de système stable : tous les pôles sont dans le demi-plan gauche

Règle pratique

• Pôles dans le demi-plan gauche → Système stable
• Pôle sur l'axe imaginaire → Système marginalement stable
• Au moins un pôle dans le demi-plan droit → Système instable

Type de réponse temporelle

La position des pôles permet de prédire le type de réponse temporelle :

Pôles réels

• Pôles réels négatifs : Réponse apériodique (exponentielle décroissante)
• Plus le pôle est proche de l'origine, plus la constante de temps est grande

Pôles complexes conjugués

• Pôles complexes conjugués : Réponse oscillatoire amortie
• L'angle $\theta$ avec l'axe réel négatif indique l'amortissement : $\cos (\theta )=m$
• Plus les pôles sont proches de l'axe imaginaire, plus les oscillations sont persistantes

Pôles complexes conjugués et coefficient d'amortissement

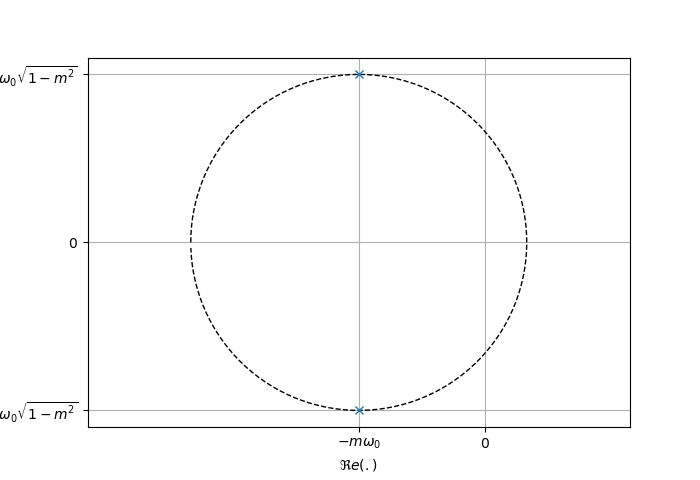
Identification des paramètres d'ordre 2

Pour un système de second ordre, les paramètres ${\omega }_0$ et $m$ peuvent être identifiés à partir des pôles.

Cas des pôles réels ($m\ge 1$)

$$\begin{array}{rl}{\omega }_0& =\sqrt{p_1\times p_2}\\ m& =-\frac{p_1+p_2}{2{\omega }_0}\end{array}$$

Cas des pôles complexes ($m<1$)

$$\begin{array}{rl}{\omega }_0& =|p_1|=\sqrt{p_1\times p_1^{\ast }}\\ m& =-\frac{\text{Re}(p_1)}{{\omega }_0}=\cos (\theta )\end{array}$$

où $\theta$ est l'angle entre le pôle et l'axe réel négatif.

Type de filtre

La présence et la position des zéros permettent d'identifier le type de filtre :

Configuration	Type de filtre
Pas de zéro	Passe-bas
Zéro à l'origine	Passe-bande
Deux zéros à l'origine	Passe-haut
Zéros sur l'axe imaginaire (±jω₀)	Réjecteur

Identification à partir de la réponse indicielle

La réponse indicielle d'un système fournit des informations directes sur son comportement temporel.

Systèmes de premier ordre

Pour un système de premier ordre, la réponse indicielle d'un passe-bas s'exprime :

$$y(t)=T_{0}E(1-e^{-t/\tau })$$

Méthode d'identification

1. Gain statique : $T_0=\frac{y(\mathrm{\infty })}{E}$

2. Constante de temps : Plusieurs méthodes possibles

   • À $t=\tau$, la sortie atteint 63.2% de sa valeur finale
   • À $t=3\tau$, la sortie atteint 95% de sa valeur finale (temps de réponse à 5%)
   • Méthode de la tangente à l'origine

Systèmes de second ordre

Pour un système de second ordre de type passe-bas, l'identification dépend du régime.

Identification du type de régime

Observer la réponse indicielle permet de déterminer le coefficient d'amortissement :

• Pas de dépassement → $m\ge 1$ (régime apériodique)
• Présence d'oscillations → $m<1$ (régime pseudo-périodique)

Cas pseudo-périodique ($m<1$)

Méthode 1 : Dépassement et valeur finale

1. Gain statique : $T_0=\frac{y(\mathrm{\infty })}{E}$

2. Dépassement relatif :

$$D_r=\frac{y_{max}-y(\mathrm{\infty })}{y(\mathrm{\infty })}=e^{-\frac{\pi m}{\sqrt{1-m^2}}}$$

En inversant cette relation :

$$m=\frac{-\ln (D_r)}{\sqrt{{\pi }^2+{\ln }^2(D_r)}}$$

3. Pseudo-période : Mesurer le temps $T_p$ entre deux pics successifs

$$T_p=\frac{2\pi }{{\omega }_0\sqrt{1-m^2}}$$

Une fois $m$ connu, on peut déterminer :

$${\omega }_0=\frac{2\pi }{T_p\sqrt{1-m^2}}$$

Méthode 2 : Ratio de dépassements successifs

Pour deux dépassements consécutifs $y_1$ et $y_2$ de même signe :

$$R=\frac{|y_1-y(\mathrm{\infty })|}{|y_2-y(\mathrm{\infty })|}=e^{\frac{2\pi m}{\sqrt{1-m^2}}}$$

Lorsque $m\ll 1$ :

$$m\approx \frac{\ln (R)}{2\pi }$$

Méthode 3 : Utilisation d'abaques

Pour des mesures plus rapides, utiliser les abaques interactives qui donnent directement la relation entre :

• $D_r(\mathrm{\%})$ et $m$
• ${\omega }_0{t}_r$ et $m$

Cas apériodique ($m>1$)

L'identification est plus complexe. Une approche consiste à :

1. Identifier le gain statique $T_0$
2. Ajuster numériquement les paramètres ${\omega }_0$ et $m$ pour faire correspondre la réponse mesurée

Exemple d'identification

Considérons une réponse indicielle avec :

• Amplitude d'entrée : $E=1$ V
• Valeur finale : $y(\mathrm{\infty })=2$ V
• Premier maximum : $y_{max}=2.4$ V
• Pseudo-période : $T_p=0.01$ s

Étape 1 : Gain statique

$$T_0=\frac{y(\mathrm{\infty })}{E}=2$$

Étape 2 : Dépassement relatif

$$D_r=\frac{2.4-2}{2}=0.2=20\mathrm{\%}$$

Étape 3 : Coefficient d'amortissement

$$m=\frac{-\ln (0.2)}{\sqrt{{\pi }^2+{\ln }^2(0.2)}}\approx 0.456$$

Étape 4 : Pulsation propre

$${\omega }_0=\frac{2\pi }{T_p\sqrt{1-m^2}}=\frac{2\pi }{0.01\sqrt{1-{0.456}^2}}\approx 704\text{ rad/s}$$

Identification à partir de la réponse fréquentielle

Le diagramme de Bode permet d'identifier directement les caractéristiques fréquentielles du système.

Type de filtre

Le type de filtre se détermine par observation du comportement asymptotique :

Comportement BF	Comportement HF	Type
Constant	$-40$ dB/déc	Passe-bas 2nd ordre
$+40$ dB/déc	Constant	Passe-haut 2nd ordre
$+20$ dB/déc	$-20$ dB/déc	Passe-bande 2nd ordre
Constant (avec creux)	Constant	Réjecteur 2nd ordre

Systèmes de premier ordre

Passe-bas

1. Gain statique : Lire $|H(j0)|$ en basse fréquence (en dB ou naturel)

2. Fréquence de coupure : Fréquence où $|H(j{\omega }_c)|=\frac{T_0}{\sqrt{2}}$ (soit -3 dB du gain statique)

3. Constante de temps : $\tau =\frac{1}{{\omega }_c}$

Passe-haut

1. Gain haute fréquence : Lire $|H(j\mathrm{\infty })|$ en haute fréquence

2. Fréquence de coupure : Fréquence où $|H(j{\omega }_c)|=\frac{T_{\mathrm{\infty }}}{\sqrt{2}}$

Systèmes de second ordre

Identification du gain

Selon le type de filtre :

• Passe-bas : $T_0=|H(j0)|$ (gain basse fréquence)
• Passe-haut : $T_{\mathrm{\infty }}=|H(j\mathrm{\infty })|$ (gain haute fréquence)
• Passe-bande : $T_m=|H(j{\omega }_0)|$ (gain à la pulsation propre)

Identification de la pulsation propre

Méthode 1 : Intersection des asymptotes

Les asymptotes basse fréquence et haute fréquence se croisent à la pulsation propre ${\omega }_0$.

Méthode 2 : Maximum de résonance (si $m<0.7$)

Si le système présente un pic de résonance :

• Passe-bas : ${\omega }_r={\omega }_0\sqrt{1-2m^2}$
• Passe-haut : ${\omega }_r=\frac{{\omega }_0}{\sqrt{1-2m^2}}$

Méthode 3 : Valeur à ${\omega }_0$

Pour tous les types, à la pulsation propre :

$$|H(j{\omega }_0)|=\frac{|N(j{\omega }_0)|}{2m}$$

Identification du coefficient d'amortissement

Méthode 1 : À partir de la résonance

Si $m<0.7$, le système présente une résonance. Pour un passe-bas :

$$|H(j{\omega }_r)|=\frac{T_0}{2m\sqrt{1-m^2}}$$

En résolvant :

$$m=\frac{1}{\sqrt{2}}\sqrt{1-{\left(\frac{{\omega }_r}{{\omega }_0}\right)}^2}$$

Méthode 2 : Valeur à ${\omega }_0$

Une fois ${\omega }_0$ identifié, évaluer $|H(j{\omega }_0)|$ :

$$m=\frac{|N(j{\omega }_0)|}{2|H(j{\omega }_0)|}$$

Pour un passe-bas : $m=\frac{T_0}{2|H(j{\omega }_0)|}$

Méthode 3 : Bande passante (pour passe-bande)

Pour un filtre passe-bande, la bande passante à -3 dB est :

$$\mathrm{\Delta }\omega =2m{\omega }_0$$

Donc :

$$m=\frac{\mathrm{\Delta }\omega }{2{\omega }_0}$$

Exemple d'identification

Soit un filtre dont le diagramme de Bode montre :

• Gain basse fréquence : $T_0=10$ (20 dB)
• Pic de résonance à $f_r=1000$ Hz avec $|H(j{\omega }_r)|=25$ (28 dB)
• Pente haute fréquence : -40 dB/déc

Identification :

1. Type : Passe-bas de 2nd ordre (gain constant en BF, -40 dB/déc en HF)

2. Gain statique : $T_0=10$

3. Coefficient d'amortissement (à partir du pic) :

   $$\frac{T_0}{2m\sqrt{1-m^2}}=25\Rightarrow m\approx 0.22$$

4. Pulsation propre :

   $${\omega }_r={\omega }_0\sqrt{1-2m^2}\Rightarrow {\omega }_0=\frac{{\omega }_r}{\sqrt{1-2m^2}}\approx 6500\text{ rad/s}$$

Méthodologie générale

Pour caractériser un système inconnu :

1. Observer la représentation disponible (pôles/zéros, indicielle, Bode)

2. Identifier l'ordre du système (nombre de pôles)

3. Déterminer le type (passe-bas, passe-haut, etc.)

4. Extraire les paramètres selon la méthode appropriée

5. Vérifier la cohérence : Les paramètres identifiés doivent être cohérents entre les différentes représentations

6. Valider par simulation : Comparer les réponses simulées avec les mesures

Validation croisée

Il est recommandé d'utiliser plusieurs méthodes d'identification pour valider les résultats. Par exemple, les paramètres ${\omega }_0$ et $m$ identifiés à partir de la réponse indicielle doivent donner le même diagramme de Bode que celui mesuré.