Rappels Mathématiques

Nombres Complexes

Notons $j$ l'imaginaire pur tel que $j^2=-1$ et $\mathbb{C}$ le corps des complexes.

Forme algébrique

Tout nombre complexe $z\in \mathbb{C}$ s'écrit sous la forme :

$$z=a+jb$$

• $a=\mathrm{\Re }e(z)$ correspond à la partie réelle,
• $b=\mathrm{\Im }m(z)$ correspond à la partie imaginaire.

Complexe Conjugué

On appelle conjugué de $z$ le nombre complexe

$$z^{\ast }=a-jb$$

Exponentielle Complexe

L'exponentielle complexe est définie par

$$e^{j\theta }=\cos (\theta )+j\sin (\theta )$$

• Multiplication : La multiplication de deux exponentielles complexes donne : $e^{j{\theta }_1}{e}^{j{\theta }_2}=e^{j({\theta }_1+{\theta }_2)}$,
• Conjugaison : Le conjugué d'une exponentielle complexe est égal à : ${\left(e^{j\theta }\right)}^{\ast }=e^{-j\theta }$,
• Périodicité: L'exponentielle complexe est $2\pi$-périodique,
• Formules d'Euler : Les formules d'Euler permettent d'exprimer le cosinus ou le sinus à partie de l'exponentielle complexe

$$\begin{array}{r}\cos (\theta )=\mathrm{\Re }e(e^{j\theta })=\frac{1}{2}(e^{j\theta }+e^{-j\theta })\\ \sin (\theta )=\mathrm{\Im }m(e^{j\theta })=\frac{1}{2j}(e^{j\theta }-e^{-j\theta })\end{array}$$

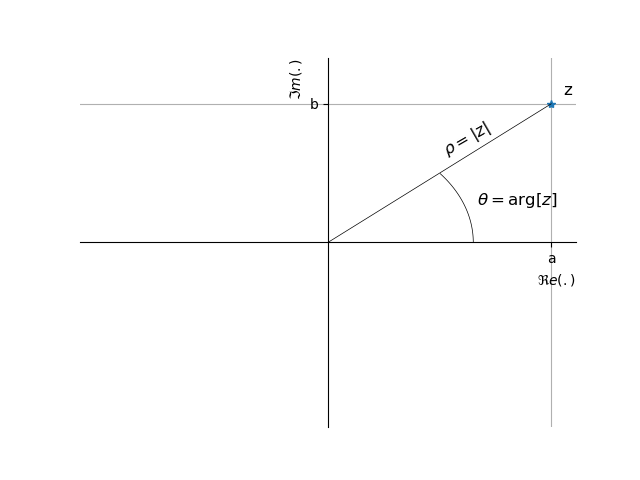
Forme Polaire

Tout nombre complexe $z\in \mathbb{C}$ non nul peut s'écrire sous la forme :

$$z=\rho e^{j\theta }$$

• $\rho =|z|$ correspond au module,
• $\theta =\arg [z]$ correspond à l'argument (modulo $2\pi$).

Propriétés

Soit deux complexes $z_1$ et $z_2$.

• Le module et l'argument de $z=z_1{z}_2$ sont donnés par :

$$\begin{array}{rl}|z|& =|z_1|\times |z_2|\\ \arg [z]& =\arg [z_1]+\arg [z_2]\end{array}$$

• Le module et l'argument de $z=z_1/z_2$ sont donnés par :

$$\begin{array}{rl}|z|& =\frac{|z_1|}{|z_2|}\\ \arg [z]& =\arg [z_1]-\arg [z_2]\end{array}$$

Conversion

Soit un nombre complexe $z=a+jb$, alors

$$\begin{array}{rl}|z|& =\sqrt{a^2+b^2}\\ \theta & =\{\begin{array}{lc}\arctan (b/a)& \text{, si }a>0,\\ \pi +\arctan (b/a)& \text{, si }a<0.\end{array}\end{array}$$

Polynômes

Forme générale

Modèle Mathématique

Un polynôme de degré $n$ est décrit par l'équation suivante :

$$p(x)=a_n{x}^n+\cdots +a_{1}x+a_0$$

• $n$ correspond au degré du polynôme,
• $a_l$ correspondent aux coefficients du polynôme.

Racines

Les racines d'un polynôme de degré $n$ correspondent aux solutions de l'équation polynomiale suivante :

$$p(x)=0$$

Lorsque les coefficients $a_l$ sont réels et non nuls, le polynôme $p(x)$ possède au plus $n$ racines. Ces racines peuvent être réelles ou complexes.

Cas du degré 2

Modèle Mathématique

Un polynôme de degré 2 est décrit par l'équation suivante :

$$p(x)=a{x}^2+bx+c$$

Racines

L'expression des racines s'obtient en évaluant le discriminant :

$$\mathrm{\Delta }=b^2-4ac$$

• Si $\mathrm{\Delta }>0$, le polynôme possède deux racines réelles distinctes :

$$\begin{array}{r}{x}_1=\frac{-b+\sqrt{\mathrm{\Delta }}}{2a}\\ x_2=\frac{-b-\sqrt{\mathrm{\Delta }}}{2a}\end{array}$$

• Si $\mathrm{\Delta }=0$, le polynôme possède une racine double réelle :

$$x_1=x_2=-\frac{b}{2a}$$

• Si $\mathrm{\Delta }<0$, le polynôme possède deux racines complexes distinctes :

$$\begin{array}{r}{x}_1=\frac{-b+j\sqrt{-\mathrm{\Delta }}}{2a}\\ x_2=\frac{-b-j\sqrt{-\mathrm{\Delta }}}{2a}\end{array}$$