Identification des filtres d'ordre 2

• Liste des AAvs concernés: AAv3

Fonctions de Transfert

Formes Canoniques

On rappelle les formes canoniques des fonctions de transfert ($T_i\in \mathbb{R}$, $m\in {\mathbb{R}}^{+}$ et ${\omega }_0\in {\mathbb{R}}^{+}$)

• Filtre Passe-bas

$$H_{LP}(s)=\frac{T_i}{\frac{1}{{\omega }_0^2}{s}^2+\frac{2m}{{\omega }_0}s+1}$$

• Filtre Passe-bande

$$H_{BP}(s)=\frac{T_i\frac{p}{{\omega }_0}}{\frac{1}{{\omega }_0^2}{s}^2+\frac{2m}{{\omega }_0}s+1}$$

• Filtre Passe-haut

$$H_{HP}(s)=\frac{T_i\frac{s^2}{{\omega }_0^2}}{\frac{1}{{\omega }_0^2}{s}^2+\frac{2m}{{\omega }_0}s+1}$$

Propriétés

• $|T_i|$ représente le point d’intersection des asymptotes,
• $|H(j{\omega }_0)|=\frac{|T_i|}{2m}$
• ${\omega }_0$ est la pulsation de symétrie de la phase

Identification à partir du diagramme des pôles et des zéros

Cas où $m>1$

1. Relevé des deux pôles réels $p_1$ et $p_2$
2. Détermination de ${\omega }_0$:

$${\omega }_0=\sqrt{p_1{p}_2}$$

3. Détermination du facteur d'amortissement:

$$m=-\frac{p_1+p_2}{2{\omega }_0}$$

Cas où $m<1$

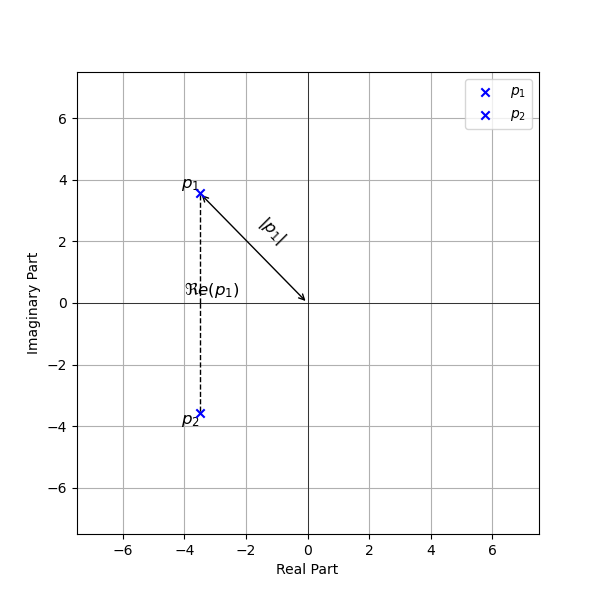
1. Relevé des deux pôles complexes-conjugués $p_1$ et $p_2=p_1^{\ast }$
2. Détermination de ${\omega }_0$:

$${\omega }_0=|p_1|$$

3. Détermination du facteur d'amortissement:

$$m=-\frac{\mathrm{\Re }e(p_1)}{{\omega }_0}$$

Identification à partir du Diagramme de Bode

1. Détermination de ${\omega }_0$:

   • Identifier le point de symétrie de la phase.
   • Relever la valeur de la pulsation, notée ${\omega }_0$, en ce point.

2. Détermination $T_i$

   • Si le filtre est un passe-bas ou un passe-haut, relever tout simplement le module $|H(j\omega )|$ de l’asymptote basse ou haute fréquence.
   • Si le filtre est un passe-bande, relever la valeur du module $H(j\omega )$ pour $\omega ={\omega }_0/10$ et $\omega =10{\omega }_0$ (on doit être dans la zone où la courbe de module suit les asymptotes). En déduire la valeur de $|T_i|$ par prolongement en exploitant la valeur de la pente ($+1$ ou $-1$)

3. Détermination de $m$ à partir du point d'intersection des asymptotes du module :

   • Relever le module de la fonction de transfert en ${\omega }_0$.
   • Utiliser la relation $|H(j{\omega }_0)|=\frac{|T_i|}{2m}$ pour déterminer la valeur de m.

4. [uniquement pour le filtre passe-bande] Détermination de $m$ à partir de la bande passante à $-3$ dB:

   • Relever les 2 pulsations délimitant la bande passante à $-3$ dB c-à-d les fréquences ${\omega }_c$ respectant la condition :
   $$|H(j{\omega }_c)|=\frac{|T_{max}|}{\sqrt{2}}$$
   • déterminer $m$ en exploitant le fait que ${\mathrm{\Delta }}_{\omega }={\omega }_{c2}-{\omega }_{c1}=2m{\omega }_0$.

Identification à partir de la Réponse Indicielle

Approche uniquement applicable si $m\ll 1$

1. Identification de $T_i$
   • [passe-bas] Mesurer la valeur du régime permanent $y(\mathrm{\infty })$. Déterminer la valeur de $T_i$ en utilisant le fait que $T_i=s(\mathrm{\infty })/E$ où $E$ correspond à l'amplitude de l'échelon.
   • [passe-haut] Mesurer le saut de tension en sortie du filtre à $t=0^{+}$. Déterminer la valeur de $T_i$ en utilisant le fait que $T_i=s(0^{+})/E$ où $E$ correspond à l'amplitude de l'échelon.
2. Identification de $m$
   • Mesurer le rapport $R$ de deux dépassements successifs par rapport à la valeur du régime permanent et «distants» d’une pseudo-période ($R>1$).
   • Determiner la valeur de $m$ en exploitant le fait que $m\approx \frac{\ln (R)}{2\pi }$ lorsque $R\gg 1$
3. Identification de ${\omega }_0$
   • Mesurer la pseudo-période $T_p$ des oscillations de la réponse.
   • Déterminer la valeur de ${\omega }_0$ en exploitant le fait que ${\omega }_p={\omega }_0\sqrt{1-m^2}$