Synthèse d'un filtre passe-bande

Ce tutorial montre le process complet pour synthétiser un filtre d'ordre N à partir d'un cahier des charges. La méthodologie décrite ici est applicable à n'importe quel filtre.

Cahier des charges

• Type de filtre: passe-bande,
• Technique de synthèse: Butterworth,
• Bande passante : $\omega \in [900,1111]$ rad/s,
• Bande rejetée : $\omega \in [0,500[\cup [2000,+\mathrm{\infty }[$ rad/s,
• Atténuation maximale dans la bande passante: $3$ dB,
• Atténuation minimale dans la bande rejetée: $40$ dB.

Code

Dans ce tutorial, nous utiliserons un fichier tools.py avec le code suivant :

import matplotlib.pyplot as plt

def plot_pzmap(ax, z, p):
    ax.plot(p.real,p.imag,'x')
    ax.plot(z.real,z.imag,'o')
    ax.set_xlabel("Re (.)")
    ax.set_ylabel("Im (.)")
    ax.axis("equal")
    ax.grid()

def plot_prototype(ax, type, wc, Tc, ws, Ts):
    xmin, xmax = ax.get_xlim()
    ymin, ymax = ax.get_ylim()

    if type == "LP":
        polygon_data1 = [[xmin,Tc], [wc,Tc], [wc,ymin], [xmin,ymin]]
        polygon_data2 = [[xmin,ymax], [xmin,1], [ws,1], [ws,Ts], [xmax,Ts], [xmax,ymax], [xmin,ymax]]
    if type == "BP":
        polygon_data1 = [[wc[0], ymin], [wc[0],Tc], [wc[1],Tc], [wc[1],ymin], [wc[0], ymin]]
        polygon_data2 = [[xmin,Ts], [ws[0],Ts], [ws[0],1], [ws[1],1], [ws[1],Ts], [xmax,Ts], [xmax,ymax], [xmin,ymax], [xmin,Ts]]

    options = {"fill": False,"closed": True,"color": 'b',"hatch": "/"} 
    patch1 = plt.Polygon(polygon_data1,**options)
    patch2 = plt.Polygon(polygon_data2,**options)

    ax.add_patch(patch1)
    ax.add_patch(patch2)
    ax.set_xscale('log')
    ax.set_yscale('log')
    ax.set_xlabel("pulsation (rad/s)")
    ax.set_ylabel("module")

Détermination du Gabarit Normalisé

Dans un premier temps, nous allons revenir à la conception d'un filtre passe-bas normalisé (${\omega }_c=1$ rad/s). Pour réaliser cette étape de normalisation, nous allons utiliser la formule liant la pulsation normalisée $\omega$ et la pulsation dénormalisée $\hat{\omega }$.

$$\omega =\frac{{\hat{\omega }}^2-{\omega }_0^2}{\hat{\omega }\mathrm{\Delta }\omega }$$

Application Numérique

• Bande passante: $\mathrm{\Delta }\omega =1111-900=211$ rad/s.
• Pulsation centrale : ${\omega }_0=\sqrt{900\times 1111}=1000$ rad/s.
• Valeur du module en $\hat{\omega }=1111$ rad/s: $T_c={10}^{-3/20}=0.707$,
• Valeur du module en $\hat{\omega }=2000$ rad/s: $T_s={10}^{-40/20}=0.01$.

En utilisant la formule, nous obtenons :

$$\begin{array}{rl}{\omega }_c& =\frac{{1111}^2-{1000}^2}{1111\times 211}\approx 1rad/s\\ {\omega }_s& =\frac{{2000}^2-{1000}^2}{2000\times 211}\approx 7.11rad/s\end{array}$$

Représentation du Gabarit

Code

import matplotlib.pyplot as plt
from tools import plot_prototype

fig, axs = plt.subplots(1, 2, figsize=(10, 4)) 

# Bandpass filter
ax0 = axs[0]
ax0.set_xlim([100, 10000])
ax0.set_ylim([0.001, 2])
ax0.set_title("filtre BP")

wc = [900, 1111]
ws = [500, 2000]
Tc = 0.707
Ts = 0.01
plot_prototype(ax0, "BP", wc, Tc, ws, Ts)

# Normalized Lowpass filter
ax1 = axs[1]
ax1.set_xlim([0.1, 100])
ax1.set_ylim([0.001, 2])
ax1.set_title("filtre LP normalisé")

wc_norm = 1
ws_norm = 7.11
plot_prototype(ax1, "LP", wc_norm, Tc, ws_norm, Ts)
fig.tight_layout()
plt.show()

Courbes

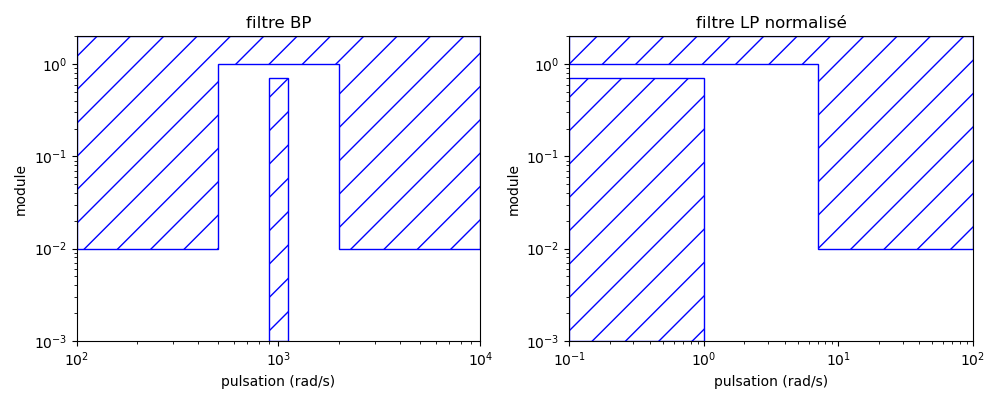
Détermination de l'ordre

Il est possible de déterminer l'ordre du filtre passe-bas normalisé en utilisant le comportement asymptotique :

$$N=\lceil -\frac{\ln \left(\frac{0.707}{0.01}\right)}{\ln \left(\frac{1}{7.11}\right)}\rceil =3$$

Synthèse du Filtre Normalisé

Pour synthétiser le filtre, nous allons utiliser la technique de synthèse de Butterworth. La fonction de transfert du filtre normalisé peut s'exprimer sous la forme factorisée suivante (zpk):

$$H_n(s)=k\frac{\prod _{l=1}^3(s-z_l)}{\prod _{l=1}^3(s-p_l)}$$

Il est possible d'obtenir les pôles $p_l$ et les zéros $z_l$ ainsi que le gain k du filtre normalisé en utilisant `scipy`:

z,p,k  =  butter(3, 1, "low", analog=True, output="zpk")

Nous obtenons les paramètres suivants:

• zéros: $z_l=\{\}$,
• pôles: $p_l=\{-0.5+0.8660254,-1,-0.5-0.8660254j\}$,
• gain: $k=1$

Dénormalisation du Filtre

Pour dénormaliser le filtre, nous allons opérer un mapping des pôles et zéros. Dans le cas d'un passe-bande, le mapping des pôles est donné par :

$$\begin{array}{rl}{\hat{p}}_l& =\alpha p_l\pm \sqrt{{\alpha }^2{p}_l^2-{\omega }_0^2}\end{array}$$

• $\alpha =\mathrm{\Delta }\omega /2=211/2=105.5$ rad/s désigne la moitié de la bande passante,
• $p_l$ correspond aux pôles du filtre normalisé,
• ${\hat{p}}_l$ correspond aux pôles du filtre dénormalisé.

Après dénormalisation, nous obtenons un filtre d'ordre $2N=6$. Pour conserver un gain maximum unitaire dans la bande passante, il est également nécessaire de changer le coefficient $k$ de la manière suivante:

$$\hat{k}=k(\mathrm{\Delta }\omega {)}^N$$

Application Numérique

Après dénormalisation, nous obtenons un filtre d'ordre 6 avec les paramètres suivants :

1. zéros: 3 zéros en 0 (filtre passe-bande d'ordre 6)

   • ${\hat{z}}_l=\{0,0,0\}$,

2. pôles: 3 paires de pôles complexes-conjugués

   • ${\hat{p}}_1=-47.943-911.424j$ et ${\hat{p}}_1^{\ast }=-47.943+911.424j$,
   • ${\hat{p}}_2=-57.556-1094.155j$ et ${\hat{p}}_2^{\ast }=-57.556+1094.155j$
   • ${\hat{p}}_3=-105.5-994.419j$ et ${\hat{p}}_3^{\ast }=-105.5+994.419j$,

3. gain $k$:

   • $\hat{k}=1\times (211{)}^3=9393931$

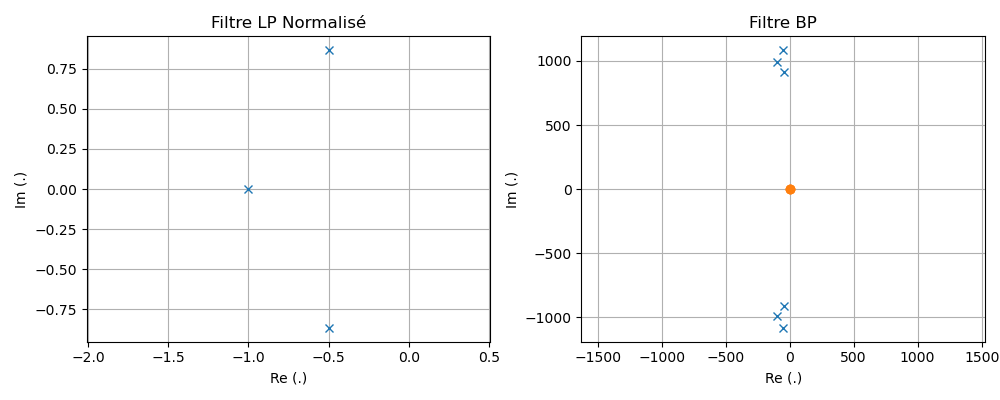
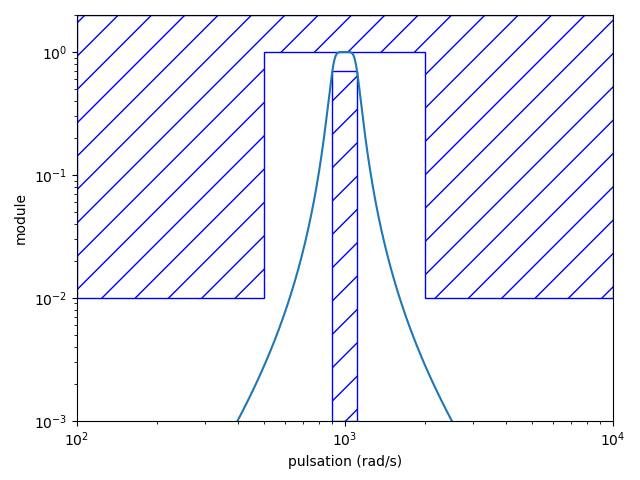
Vérification

Pour vérifier que le filtre dénormalisé respecte bien les contraintes du cahier des charges, une solution naturelle consiste à afficher la réponse fréquentielle du filtre dénormalisé.

$$H(s)=\hat{k}\frac{\prod _{l=1}^3(s-{\hat{z}}_l)}{\prod _{l=1}^6(s-{\hat{p}}_l)}$$

Code

import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import lti, butter 
from tools import plot_prototype

k2 = 9393931
z2 = [0.+0.j, 0.+0.j, 0.+0.j]
p2 = [ -47.943-911.374j, -105.5-994.369j, -47.943 +911.374j, -57.556+1094.106j, -105.5 +994.369j, -57.556-1094.106j]
H = lti(z2, p2, k2)
w, Hjw = H.freqresp()

fig = plt.figure()
w, Hjw = H.freqresp()
plt.loglog(w, np.abs(Hjw))
plt.xlabel("pulsation (rad/s)")
plt.ylabel("module")
ax = plt.gca()

wc = [900, 1111]
ws = [500, 2000]
Tc = 0.707
Ts = 0.01
ax.set_xlim([100, 10000])
ax.set_ylim([0.001, 2])
plot_prototype(ax, "BP", wc, Tc, ws, Ts)
fig.tight_layout()
plt.show()

Résultat