Analyse d'un Circuit de Premier Ordre

Dans ce tutorial, nous allons réaliser une analyse complète d'un circuit de premier ordre (RC_LP). Le circuit considéré est le suivant :

Analyse Théorique

Fonction de Transfert

La fonction de transfert du circuit s'obtient en utilisant le pont diviseur de tension. En notant $y(t)$ la sortie $V_{out}(t)$ et $x(t)$ l'entrée $V_{in}(t)$, nous obtenons dans le domaine de Laplace:

$$\begin{array}{rl}S(s)& =\frac{Z_c}{Z_c+Z_r}X(s)\\ & =\frac{\frac{1}{Cp}}{\frac{1}{Cp}+R}S(s)\\ & =\frac{1}{RCp+1}X(s)\end{array}$$

Nous en déduisons que la fonction de transfert du système est égal à

$$H(s)=\frac{S(s)}{X(s)}=\frac{1}{RCp+1}$$

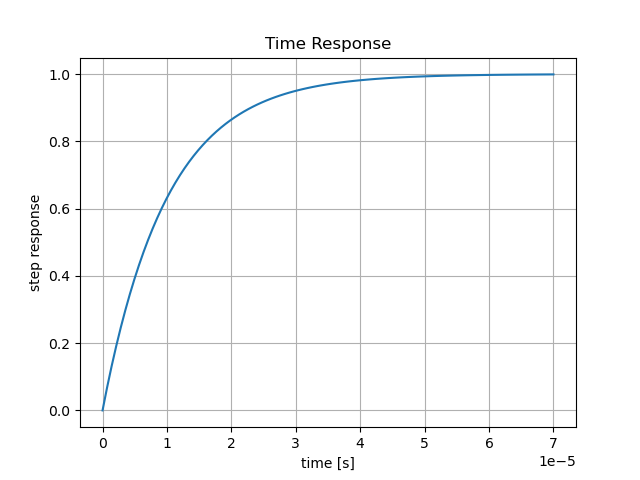
Réponse Indicielle

Le système peut être décrit dans le domaine temporelle par l'équation suivante :

$$RC\frac{dy(t)}{dt}+y(t)=x(t)$$

Nous allons nous intéresser à la sortie lorsque l'entrée est un échelon d'amplitude E

$$\begin{array}{r}x(t)=\{\begin{array}{cc}E& \text{ si }t\ge 0\\ 0& \text{ ailleurs}\end{array}\end{array}$$

La sortie du système est supposée initialement nulle c-a-d $y(0^{-})=0$.

Expression de la solution complète

1. Détermination des racines de l'équation caractéristique :

$$RCp+1=0\Rightarrow p=-\frac{1}{RC}$$

2. Détermination du régime Libre :

$$y_l(t)=\lambda e^{-\frac{1}{RC}t}$$

3. Détermination du Régime Forcé : Lorsque l'entrée est un échelon d'amplitude E, le regime permanent s'exprime sous la forme $y_p(t)=\alpha u(t)$. La valeur de $\alpha$ s'obtient en injectant l'expression du regime permanent dans l'équation différentielle. Pour $t\ge 0$, nous obtenons :

$$y_p(t)=E$$

4. Détermination de la Solution Complète: Pour $t\ge 0$, nous obtenons finalement

$$y(t)=y_l(t)+y_p(t)=\lambda e^{-\frac{1}{RC}t}+E$$

5. Exploitation des conditions initiales. La détermination de la constante d'intégration peut s'obtenir en déterminant la valeur de $y(t)$ en $t=0^{+}$. Il est possible de démontrer que $y(0^{+})=0$, ce qui implique que :

$$y(0^{+})=\lambda \times 1+E=0\Rightarrow \lambda =-E$$

Pour $t\ge 0$, nous obtenons finalement l'expression suivante :

$$y(t)=E(1-e^{-\frac{1}{RC}t})$$

Valeurs Remarquables

• Valeur initiale: $y(0^{+})=0$,
• Valeur finale: $y(\mathrm{\infty })=E$,
• Valeur maximale: $max(y(t))=E$,
• Valeur en $t=\tau =RC$, $y(\tau )=0.63E$,
• Valeur en $t=3\tau =3RC$, $y(3\tau )=0.95E$.

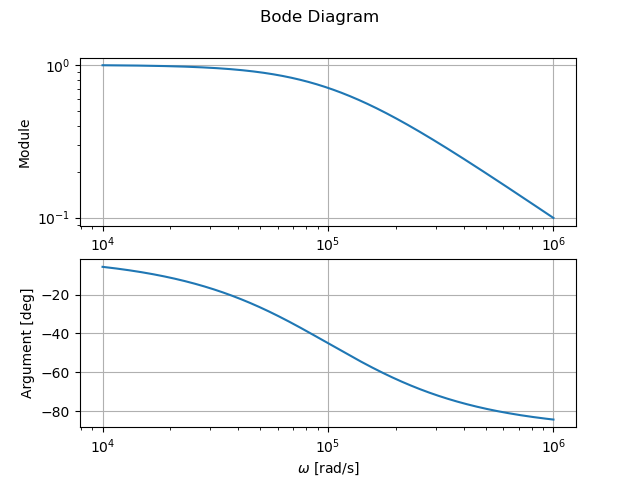
Réponse Fréquentielle

Expression

La réponse fréquentielle s'obtient en évaluant la fonction de transfert en $s=j\omega$. Mathématiquement, nous obtenons :

$$H(j\omega )=\frac{1}{jRC\omega +1}$$

• Module :

$$|H(j\omega )|=\frac{1}{\sqrt{(RC\omega {)}^2+1}}$$

• Argument :

$$\arg [H(j\omega )]=-\arctan \left(RC\omega \right)$$

Valeurs Remarquables

• Basse-Fréquence : Lorsque $\omega \to 0$,

$$\begin{array}{rl}|H(j\omega )|& \approx 1,\\ \arg [H(j\omega )]& \approx 0.\end{array}$$

• Pulsation de coupure : Lorsque $\omega ={\omega }_c=\frac{1}{RC}$,

$$\begin{array}{rl}|H(j{\omega }_c)|& =\frac{1}{\sqrt{2}},\\ \arg [H(j{\omega }_c)]& =-{45}^o.\end{array}$$

• Asymptotes Haute-Fréquences :

$$\begin{array}{rl}\underset{\omega \to \mathrm{\infty }}{lim}|H(j\omega )|& ={\left(\frac{\omega }{{\omega }_c}\right)}^{-1},\\ \underset{\omega \to \mathrm{\infty }}{lim}\arg [H(j\omega )]& =-{90}^o.\end{array}$$

Simulation Python

Code

import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import lti


class LTI_analysis():

    def lti(self):
        raise NotImplementedError("Subclasses must implement this method")

    def step(self, T=None):
        """
        Computes and plots the step response of the system (response to a unit step input).
        
        Arguments:
            T : time array (optional). If not specified, the time array is automatically generated.
        """
        H = self.lti()
        t, s = H.step(T=T)
        plt.figure("Time Response")
        plt.plot(t, s)
        plt.grid()
        plt.xlabel('time [s]')
        plt.ylabel('step response')
        return t, s

    def freqresp(self, w=None):
        """
        Computes and plots the frequency response of the system.
        
        Arguments:
            w : frequency array (in rad/s). If not specified, frequencies are automatically generated.
        """
        H = self.lti()
        w, Hjw = H.freqresp(w=w)
        fig, axs = plt.subplots(2, 1)
        fig.suptitle("Bode Diagram")
        axs[0].loglog(w, np.abs(Hjw))
        axs[0].set_xlabel("$\omega$ [rad/s]")
        axs[0].set_ylabel("Module")
        axs[0].grid()
        axs[1].semilogx(w, 180*np.angle(Hjw)/np.pi)
        axs[1].set_xlabel("$\omega$ [rad/s]")
        axs[1].set_ylabel("Argument [deg]")
        axs[1].grid()
        return w, Hjw


class RC_LP_1st_order(LTI_analysis):
    """
    Class representing a first-order RC low-pass filter.
    This filter is modeled by a linear time-invariant (LTI) system.
    """

    def __init__(self, R=10**3, C=10**-9):
        """
        Initializes the class with a resistance R (in ohms) and a capacitance C (in farads).
        """
        self.R = R
        self.C = C

    def lti(self):
        """
        Creates a linear time-invariant (LTI) model for the RC circuit.
        """
        tau = self.R*self.C
        return lti([1], [tau, 1])


if __name__ == "__main__":
    filter = RC_LP_1st_order(R=10**4, C=10**-9)
    filter.step()
    filter.freqresp()
    plt.show()

Courbes